ALS는 행렬 분해를 활용한 대표적인 추천 알고리즘입니다.

추천 시스템을 구축하기 위한 첫 출발점으로는 matrix factorization에 기반을 둔 모델을 많이 활용합니다. 그 이유는 단일 모델로서 성능도 좋고, 무엇보다 데이터 파이프라인이 간단하고 서빙이 편리하기 때문이라고 생각합니다. matrix factorization 기법을 활용한 추천 모델은 매우 다양한데요. 대표적으로 SVD, SGD, ALS 등을 꼽을 수 있을 것 같습니다. 본 글에서는 ALS를 소개한 논문을 정리하고, 본 논문에서는 생략되어 있는 수식 유도 과정을 추가로 정리 하고자 합니다. 논문의 제목은 “Collaborative Filtering for Implicit Feedback Datasets” 입니다. 제목에서도 유추가 가능하지만 implicit data에 matrix factorization 기법을 어떻게 적용할지에 대한 간단한 아이디어를 제안한 논문입니다.

본 글에서 행렬과 벡터의 표기는 다음을 따릅니다.

행렬: \(\boldsymbol{X}\)
벡터: \(\boldsymbol{x}\)
벡터의 원소: \(x\)

Introduction

Characteristic of implicit data

저자는 현실 세계의 문제는 대부분 implicit data로 구성되어 있으므로 implicit data를 활용한 추천 시스템 연구가 반드시 필요하다고 주장합니다. 특히 우리가 implicit data에 주목해야 하는 이유는 implicit data가 다음의 특성을 가지고 있기 때문입니다.

No negative feedback
explicit data는 유저가 특정 아이템을 좋아하는지(like) 싫어하는지(dislike)를 명확하게 알 수 있고, 이러한 풍부한 정보를 활용하여 추천 시스템을 모델링 할 수 있습니다. 저자의 표현을 빌리면 유저의 선호에 대한 balanced picture를 활용할 수 있다는 것입니다. 그러나 implicit data는 유저가 특정 아이템과 interaction이 있었는지 없었는지 여부만 알 수 있습니다. 예를 들어 어떤 유저가 유튜브에서 무한도전 영상을 보지 않았다면, 무한도전 영상을 싫어해서 보지 않은 것인지 그 영상의 존재 여부를 몰라서 그런 것인지를 추측하기가 어렵다는 것이죠.
또한 explicit data나 implicit data 모두 user-rating 행렬의 대부분의 값들이 missing value로서 존재합니다. 일반적으로 explicit data로 추천 시스템 모델링을 할 때는 missing value를 탈락시키고 관측된 데이터로만 모델링을 진행합니다. explicit data는 관측된 데이터 안에서도 선호 또는 비선호 정보가 모두 있기 때문에 논리적인 비약이 발생하지 않습니다. 그러나 implicit data의 경우 missing value를 탈락 시킨후 모델링을 진행하면 positive feedback 정보만 활용하여 모델링을 진행하게 되는 꼴이 되버립니다. 저자는 이를 ‘misrepresenting the full user profile’이라고 표현하였습니다.
Implicit feedback is inherently noisy
우리는 유저의 implicit feedbac을 통해 정확한 유저의 선호를 알 수 없습니다. 제가 인터넷에서 코트 한벌을 구입 했다고 가정해볼게요. 물론 심사숙고 끝에 코트를 구입한 것이므로, 구매 행위는 positive feedback이라고 생각할 수도 있습니다. 그러나 만일 제가 코트를 받아보고 원단 재질에 실망 했다면 구매 행위가 negative feedback이 될 수 있는 여지도 있죠. 비슷하게 어떤 유저의 영상 시청 시간이 길다는 것이 무조건 positive feedback은 아닐 것입니다. 영상을 틀어 놓고 잠이 들었을 수도 있는 것이죠.
Numerical value of implicit feedback indicates confidence
explicit feedback은 유저의 preference를 나타내지만, implicit feedback은 단순히 frequency of actions를 나타냅니다. 다시 말해, implicit data에서는 특정 행위의 빈도가 높다는 것이 유저가 그 아이템을 선호한다는 것을 의미하지 않는다는 것입니다. 예를 저는 가장 좋아하는 가수가 임창정인데요. 그렇다고 해서 하루에 몇 백번씩 소주 한잔을 듣지는 않습니다.
그러나 implicit feedback의 빈도가 전혀 유용하지 않다는 의미는 아닙니다. 특정 행위가 계속해서 반복 된다는 것은 특정 유저의 opinion을 반영한다는 의미가 될 수 있습니다. 정리하자면, implicit feedback의 빈도가 높다는 것은 유저가 그 아이템을 선호한다고 단정지어 말할 수는 없지만, 적어도 선호할 것이라고 주장하는 것에 대한 신뢰도(confidence)를 높여줄 수 있습니다.

Objective

이러한 implicit data의 특징을 알아 두시구요. 계속해서 다음의 두가지 논의를 중점적으로 살펴보겠습니다.

implicit data에서 confidence를 어떻게 계산할 것인가?
- \(C_{ui}\) 지표 제안
효율적인 추천 시스템을 어떻게 구현할까?
- ALS(Alternative Least Square) 제안

Latent factor collaborative filtering

추천 시스템을 구현하는 방식은 매우 다양합니다. 간단하게는 아이템 자체의 정보(e.g. 상품명)만을 이용하여 유사한 아이템을 추천하는 contents-based 추천 알고리즘이 있습니다. TF-IDF나 word2vec 기반의 추천 시스템이 대표적인 예시입니다.

한편 CF(collaborative filtering) 방식으로 추천 시스템을 구현할 수도 있습니다. CF는 유저와 아이템간의 interdependency를 분석하여 새로운 user-item 관계를 발견하기 위한 기법입니다. 쉽게 풀어쓰면 단순히 상품 자체의 정보만을 이용하는 것이 아니라 비슷한 다른 유저의 interaction 정보를 활용하여 유저와 아이템간의 내재된 관계를 발견해보겠다는 것입니다.

당연하게도 CF 기반의 추천 시스템을 구현하는 다양한 방법이 존재합니다. 그 중에서 Netflix Prize Competition에서 우수한 성적을 거둔 matrix factorization 기반의 추천 알고리즘이 많이 활용됩니다. 다른 말로 latent factor CF라고도 불립니다. 행렬 분해를 활용한 추천 시스템의 핵심은 유저와 아이템을 특정 차원의 latent factor로 잘 임베딩하는 방법을 찾는 것입니다. 아래의 그림을 통해 조금 더 자세히 설명해볼게요.

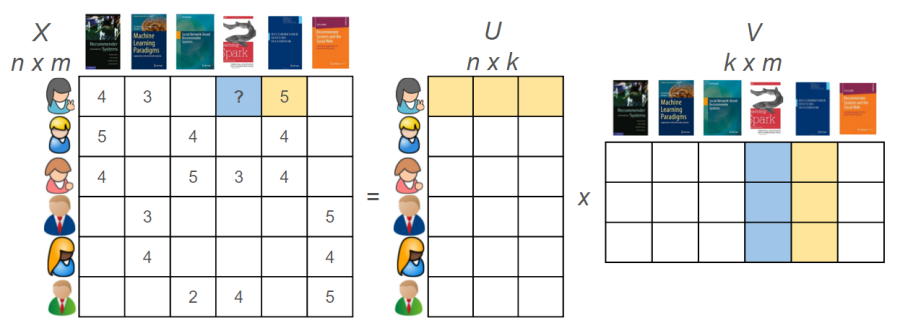
latent factor CF 알고리즘은 기본적으로 user-item 행렬 \(\boldsymbol{R} \in \mathbb{R}^{n \times m}\)을 유저 행렬 \(\boldsymbol{U}\in \mathbb{R}^{n \times k}\)와 아이템 행렬 \(\boldsymbol{V} \in \mathbb{R}^{m \times k}\)로 분해해서 표현하는 것입니다. 유저 행렬 \(\boldsymbol{U}\)와 아이템 행렬 \(\boldsymbol{V}^T\)를 곱하면 원 행렬과 똑같은 크기의 행렬로 복원할 수 있는데요. 이 행렬을 \(\hat{\boldsymbol{R}} = \boldsymbol{U}\boldsymbol{V}^T\)이라고 한다면 latent factor CF의 핵심은 \(\boldsymbol{R}\)과 \(\hat{\boldsymbol{R}}\)의 차이를 최대한 줄이는 것이 핵심이겠죠. latent factor CF를 구현하는 대표적인 알고리즘으로 SVD, SGD, ALS 등을 들 수 있는데요. 본 논문에서는 ALS를 다룹니다.

Notations

앞으로의 논의에는 많은 notation이 등장하는데요. 이에 대해 정리를 하고 가는 것이 좋을 것 같습니다. 특히 논문에 행렬 notation이 매우 헷갈릴만하게 서술 되어 있기 때문에 행렬 형상을 주의해서 살펴주시길 바랍니다.

\(m\) : 유저의 개수
\(n\) : 아이템의 개수
\(f\) : 유저와 아이템 latent vector의 차원수
\(\boldsymbol{X} \in \mathbb{R}^{m \times f}\) : \(m\)명의 유저의 latent vector \(\boldsymbol{x}_u\)를 행벡터 \(\boldsymbol{x}_u^{T}\)로 쌓은 유저 행렬.
\(\boldsymbol{Y} \in \mathbb{R}^{n \times f}\) : \(n\)개의 아이템의 latent vector \(\boldsymbol{y}_i\)를 행벡터 \(\boldsymbol{y}_i^{T}\)로 쌓은 아이템 행렬.
\(\boldsymbol{x}_u \in \mathbb{R}^f\) : 유저 \(u\)의 latent vector (열벡터)
\(\boldsymbol{y}_i \in \mathbb{R}^f\) : 아이템 \(i\)의 latent vector (열벡터)
\(\boldsymbol{p(u)} \in \mathbb{R}^n \): 유저 \(u\)의 \(n\)개의 아이템에 대한 preference \(p_{ui}\)를 나타내는 벡터
\(\boldsymbol{C^u} \in \mathbb{R}^{n \times n} \): 유저 \(u\)의 \(n\)개의 아이템에 대한 confidence \(c_{ui}\)를 나타내는 대각 행렬
\(r_{ui}\) : 유저 \(u\)의 아이템 \(i\)에 대한 observations (e.g. 구매 횟수, 시청 시간)
\(\hat{r}_{ui}\) : 유저 \(u\)의 아이템 \(i\)에 대한 예측 observations

Our model

본 논문에서 저자가 주장하는 핵심은 다음의 두가지입니다. 섹션 4에서는 계속해서 두 핵심 주장을 좀더 자세히 살펴보겠습니다. 논문에는 자세한 설명이 생략되어 있어서 저의 개인적인 의견을 덧붙여서 설명드려 보겠습니다.

implicit data의 특성에 기반하여 raw observations \(\boldsymbol{r_{ui}}\)를 preference \(\boldsymbol{p_{ui}}\)와 confidence level \(\boldsymbol{c_{ui}}\)로 변환하여 활용
global mininum으로의 수렴이 보장되는 ALS(Alternative Least Square) 알고리즘 제안

preference

저자는 먼저 유저 \(u\)가 아이템 \(i\)에 대해 intercation이 한번이라도 있었으면 \(p_{ui}=1\)로, interaction이 없었으면 \(p_{ui}=0\)으로 binarizing을 합니다.

\[p_{ui} = \begin{cases} 1 & r_{ui}>0 \\ 0 & r_{ui}=0 \end{cases}\]

일단은 interaction이 있었다는 것을 유저가 아이템을 like 한다는 징후(indication)으로 가정합니다. 반대로 말하면 interaction이 없었다는 것은 유저가 해당 아이템을 선호하지 않는다고 가정하는 것이죠. 그러나 이러한 가정은 어딘가 부족해보입니다. 당장 저자가 언급하였던 implicit data의 내재적 문제를 전혀 고려하지 못한 주장이라는 생각이 듭니다. 따라서 저자는 이를 보완하고자 confidence level이라는 지표를 추가적으로 도입합니다.

confidence level

confidence level이란 \(p_{ui}={0, 1}\) 값의 신뢰도(confidence level)를 정량화하기 위한 지표입니다. \(p_{ui}=0\)인 이유는 정말 여러가지가 있을 수 있습니다. 예를 들어서 실제로 아이템 \(i\)가 존재한다는 것을 알고 있으면서도 해당 아이템을 선호하지 않기 때문에 interaction을 하지 않았을 수도 있습니다. 이 경우는 실제로 negative feedback이죠. 그러나 유저가 아이템 \(i\)의 존재를 몰랐을 수도 있으며, 아이템 \(i\)의 비싼 가격 때문에 선호를 함에도 불구하고 interaction을 하지 않았을 수도 있죠. 따라서 interaction이 없었다는 사실 하나만으로 선호/비선호를 이분법적으로 구분하는 것은 논리적 비약입니다. 따라서 저자는 \(p_{ui}\)의 confidence level를 측정하기 위한 지표를 제안합니다.

\[c_{ui} = 1 + \alpha r_{ui}\]

먼저 이 지표를 설명하기 위한 가정 하나가 있습니다. 바로 \(r_{ui}\)값이 증가할수록 유저 \(u\)가 아이템 \(i\)를 더욱 강하게 선호한다는 것입니다. 단순히 interaction이 있었다면 선호, 없었다면 비선호 한다는 가정보다는 훨씬 납득할만한 가정이라고 생각합니다.

이제 신뢰도 지표 \(c_{ui}\)를 도입한 저자의 목적을 이해해 봅시다. 신뢰도 지표 \(c_{ui}\)는 똑같이 \(p_{ui}=1\)를 가지는 user-item 쌍에 대해서도 \(r_{ui}\)에 따른 가중치를 달리 줄 수 있다는 점에서 중요한 지표라고 생각합니다. 예를 들어 \(r_{ui}\)를 유저 \(u\)가 아이템 \(i\)를 구매한 횟수라고 한다면, \(r_{ui}=1\)인 것에 비해 \(r_{ui}=10000\)인 것이 유저 \(u\)의 아이템 \(i\)에 대한 선호도가 강하다고 상식적으로 생각할 수 있습니다.

그러나 \(c_{ui}\)를 고려하지 않는다면 \(r_{ui}=1\)인 것이나 \(r_{ui}=10000\) 모두 \(p_{ui}=1\)로 동일한 값을 갖게 되므로 선호의 강도의 차이를 반영하지 못하게 됩니다. 다시 \(c_{ui}\)를 계산하는 수식을 살펴봅시다. \(r_{ui}\)가 증가할수록 confidence level \(c_{ui}\)가 선형적으로 증가하게 됨을 확인하실 수 있습니다. 다시 말해 confidence level \(c_{ui}\) 지표를 도입함에 따라 ‘선호의 강도’를 구분할 수 있게 된 것입니다. 참고로 저자는 실험적으로 \(\alpha=40\)이 좋았다고는 하는데, 절대적인 진리는 아니라고 생각합니다. 참고용으로만 알아두시면 될 것 같습니다.

ALS

이제 저자의 두번째 핵심 주장인 ALS 알고리즘에 대해 살펴보겠습니다. ALS는 matrix factorization 기반의 알고리즘인데요. 따라서 아래의 수식이 ALS 알고리즘의 최적화 목표입니다.

\[\min_{\boldsymbol{x}*,\boldsymbol{y}*}\sum_{u, i}c_{ui}(p_{ui} - \boldsymbol{x}_{u}^{T}\boldsymbol{y}_{i})^{2} + \lambda \bigg( \sum_{u} \|\boldsymbol{x}_{u}\|^{2} + \sum_{i} \|\boldsymbol{y}_{i}\|^{2} \bigg) \tag{1}\]

먼저 \(\lambda \big( \sum_{u} \|\boldsymbol{x}_{u}\|^{2} + \sum_{i} \|\boldsymbol{y}_{i}\|^{2} \big)\)는 알고리즘의 overfitting을 방지하기 위한 일반적인 regularizing term입니다. 중요한 점은 \((1)\) 수식은 모든 유저-아이템 쌍 \(m \times n\)에 대해서 계산된다는 점입니다. 따라서 데이터 셋의 크기가 매우 크다면(\(m \times n\)이 매우 큰 숫자라면) explicit data 최적화에 주로 활용되는 SGD 등의 최적화 테크닉은 잘 작동하지 않는다고 합니다. 따라서 저자는 이러한 현실적인 문제를 극복하기 위해 효율적인 최적화 테크닉인 ALS(alternative least square)를 제안합니다.

ALS는 이름에서도 알 수 있듯이 번갈아가며 최적화를 진행한다는 것입니다. 무엇을 번갈아가며 최적화를 한다는 것일까요? 바로 유저 행렬 \(\boldsymbol{X}\)와 아이템 행렬 \(\boldsymbol{Y}\)입니다. 그렇다면 어떻게 최적화를 한다는 것일까요? 다음의 순서에 따라 최적화를 진행합니다.

Step1: 아이템 행렬 \(\boldsymbol{Y}\)를 상수로 고정하고, 유저 행렬 \(\boldsymbol{X}\)를 최적화
Step2: 유저 행렬 \(\boldsymbol{X}\)를 상수로 고정하고, 아이템 행렬 \(\boldsymbol{Y}\)를 최적화
Step3: Step1과 Step2를 원하는 횟수만큼 반복

이러한 방식의 최적화는 OLS에서 residual이 최소화되는 파라미터를 찾는 방법과 정확히 일치합니다. OLS는 global minum 값이 항상 보장되는 convex function이라고 합니다. 따라서 학습 프로세스가 진행됨에 따라 cost가 지속적으로 감소되는 것이 보장된다고 합니다. 사실 수식 \((1)\)을 최소화하는 최적의 \(\boldsymbol{x_u}\)는 다음의 solution으로 결정되어 있습니다. \(\boldsymbol{x}_u\)를 유도하는 수식은 Appendix에 자세히 적어 두겠습니다. 혹시 궁금하신 분들은 참고해주세요.

\[\boldsymbol{x}_u = (\boldsymbol{Y}^T\boldsymbol{C}^{u}\boldsymbol{Y}+ \lambda\boldsymbol{I})^{-1}\boldsymbol{Y}^T\boldsymbol{C}^{u}\boldsymbol{p(u)} \tag{2}\]

같은 방법으로 최적의 \(\boldsymbol{y}_i\)의 solution을 도출할 수 있습니다.

\[\boldsymbol{y}_i = (\boldsymbol{X}^T\boldsymbol{C}^{i}\boldsymbol{X}+ \lambda\boldsymbol{I})^{-1}\boldsymbol{X}^T\boldsymbol{C}^{i}\boldsymbol{p(i)} \tag{3}\]

이제 우리는 최적의 \(\boldsymbol{x}_u\)와 \(\boldsymbol{y}_i\)를 원하는 횟수만큼 번갈아서 계산하면 되겠습니다.

맺으며

본 논문에서 저자의 핵심 주장은 다음의 두가지입니다.

implicit data에서 preference 지표와 confidence level 지표를 도입
효율적인 행렬 최적화를 위한 ALS 제안

개인적으로는 대표적인 행렬 분해 추천 알고리즘인 ALS가 따로 논문이 존재한다는 것을 처음 알게 되었는데요. 새롭고 혁신적인 주장은 의외로 간단한 아이디어에서 시작하는 것 같습니다. 특히 행렬 분해를 OLS 방식으로 해결하는 시도가 매우 인상 깊었습니다. 그러나 이 방법도 한계가 존재한다고 생각합니다. 저는 일반적인 CF 기법과 마찬가지로 다양한 feature를 반영하지 못한다는 점을 지적하고 싶습니다. 논문을 읽어 보시면 아시겠지만 TV 시청시간, 제품 구매 횟수 등 단편적인 feature만을 예시로 계속 들고 있습니다. 이러한 단점 때문에 최근에는 다양한 feature를 구성할 수 있는 FM(Factorization Machine)이나 딥러닝 기반 추천을 도입하려는 시도가 많이 이루어지는 것 같습니다. 다음 번 추천 시스템 포스팅은 FM이나 딥러닝 기반 추천 알고리즘에 대해 다뤄보려고 합니다. 긴 글 읽어 주셔서 감사합니다.

Appendix

Step1. \(L\)을 \(\boldsymbol{x}_u\)로 편미분한 값을 구해봅시다.

\[\begin{align} \cfrac{\partial L}{\partial \boldsymbol{x}_u} &= \cfrac{\partial}{\partial \boldsymbol{x}_u}\bigg[\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 + \lambda \big( \sum_{u} \|\boldsymbol{x}_{u}\|^{2} + \sum_{i} \|\boldsymbol{y}_{i}\|^{2} \big) \bigg] \\[1em] &= \cfrac{\partial}{\partial \boldsymbol{x}_u}\bigg[\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 \bigg] + \cfrac{\partial}{\partial \boldsymbol{x}_u} \bigg[\lambda \big( \sum_{u} \|\boldsymbol{x}_{u}\|^{2} + \sum_{i} \|\boldsymbol{y}_{i}\|^{2} \big) \bigg] \\[1em] &= \begin{bmatrix} \cfrac{\partial}{\partial x_{u1}}\bigg[\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 \bigg] \\ \vdots\\ \cfrac{\partial}{\partial x_{uf}}\bigg[ \sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 \bigg] \end{bmatrix} + \cfrac{\partial}{\partial \boldsymbol{x}_u} \bigg(\lambda \sum_{u} \|\boldsymbol{x}_{u}\|^{2} \bigg) + \cfrac{\partial}{\partial x_{u}} \bigg(\lambda \sum_{i} \|\boldsymbol{y}_{i}\|^{2} \big) \bigg) \\[1em] &= \begin{bmatrix} \cfrac{\partial}{\partial x_{u1}}\bigg[\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 \bigg] \\ \vdots\\ \cfrac{\partial}{\partial x_{uf}}\bigg[ \sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 \bigg] \end{bmatrix} + \cfrac{\partial}{\partial \boldsymbol{x}_u} \bigg(\lambda \sum_{u} \|\boldsymbol{x}_{u}\|^{2} \bigg) \\[1em] &= \begin{bmatrix} \cfrac{\partial}{\partial x_{u1}}\bigg[c_{u1}(p_{u1}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_1)^2 + \cdots + c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 + \cdots + c_{un}(p_{un}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_n)^2 \bigg] \\ \vdots\\ \cfrac{\partial}{\partial x_{uf}}\bigg[c_{u1}(p_{u1}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_1)^2 + \cdots + c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)^2 + \cdots + c_{un}(p_{un}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_n)^2 \bigg] \end{bmatrix} + \begin{bmatrix} \cfrac{\partial}{\partial x_{u1}} \bigg[ \lambda(x_{u1}^2 + \cdots + x_{uf}^2) \bigg] \\ \vdots \\ \cfrac{\partial}{\partial x_{uf}}\bigg[ \lambda(x_{u1}^2 + \cdots + x_{uf}^2) \bigg] \end{bmatrix} \\[1em] &= \begin{bmatrix} -2c_{u1}(p_{u1}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_1)y_{11} - \cdots -2c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)y_{i1} - \cdots -2c_{un}(p_{un}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_n)y_{n1}\\ \vdots\\ -2c_{u1}(p_{u1}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_1)y_{1f} - \cdots -2c_{ui}(p_{ui}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_i)y_{if} - \cdots -2c_{un}(p_{un}-\boldsymbol{x}_{u}^{T}\boldsymbol{y}_n)y_{nf} \end{bmatrix} + 2\lambda \boldsymbol{x}_u \\[1em] &= \begin{bmatrix} -2c_{u1}(p_{u1}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{1})y_{11} \\ \vdots \\-2c_{u1}(p_{u1}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{1})y_{1f} \end{bmatrix} + \cdots + \begin{bmatrix} -2c_{ui}(p_{ui}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{i})y_{i1} \\ \vdots \\-2c_{ui}(p_{ui}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{i})y_{if} \end{bmatrix} + \cdots + \begin{bmatrix} -2c_{un}(p_{un}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{n})y_{n1} \\ \vdots \\ -2c_{un}(p_{un}-\boldsymbol{x}_{u}^T\boldsymbol{y}_{n})y_{nf} \end{bmatrix} + 2\lambda\boldsymbol{x}_u \\[1em] &= -2c_{u1}(p_{u1}-\boldsymbol{x}_{u}^T \boldsymbol{y}_{1}) \boldsymbol{y}_{1} + \cdots + -2c_{ui}(p_{ui}-\boldsymbol{x}_{u}^T \boldsymbol{y}_{i})\boldsymbol{y}_{i} + \cdots + -2c_{un}(p_{un}-\boldsymbol{x}_{u}^T \boldsymbol{y}_{n})\boldsymbol{y}_{n}\\[1em] &= -2\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^T\boldsymbol{y}_i)\boldsymbol{y}_i + 2\lambda \boldsymbol{x}_u \end{align}\]

Step2. 편미분 값을 0으로 놓고 수식을 전개

먼저 편미분 값 = 0으로 놓은 수식을 적어볼게요.

\[-2\sum_{i}c_{ui}(p_{ui}-\boldsymbol{x}_{u}^T\boldsymbol{y}_i)\boldsymbol{y}_i + 2\lambda \boldsymbol{x}_u = 0\]

\(c_{ui}\)를 전개해 줍니다.

\[-2\sum_{i}(c_{ui}p_{ui}-c_{ui}\boldsymbol{x}_{u}^T\boldsymbol{y}_i)\boldsymbol{y}_i + 2\lambda \boldsymbol{x}_u = 0\]

\(\boldsymbol{y_i}\)를 전개해 줍니다.

\[-2\sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i+2\sum_{i}c_{ui}\boldsymbol{x}_{u}^T\boldsymbol{y}_i\boldsymbol{y}_i + 2\lambda \boldsymbol{x}_u = 0\]

상수 \(2\)를 소거하고 식을 정리해 줍니다.

\[\sum_{i}c_{ui}(\boldsymbol{x}_{u}^T\boldsymbol{y}_i)\boldsymbol{y}_i +\lambda \boldsymbol{x}_u = \sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i\]

\(\boldsymbol{x}_u^T\boldsymbol{y}_i\)는 상수이므로 \(\boldsymbol{x}_u^T\boldsymbol{y}_i = \boldsymbol{y}_i^T\boldsymbol{x}_u\)입니다.

\[\sum_{i}c_{ui}(\boldsymbol{y}_i^T\boldsymbol{x}_{u})\boldsymbol{y}_i +\lambda \boldsymbol{x}_u = \sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i\]

\(\boldsymbol{y}_i^T\boldsymbol{x}_u\)는 상수이므로 \(\boldsymbol{y}_i\)와 자리를 바꿔도 무방합니다.

\[\sum_{i}c_{ui}\boldsymbol{y}_i\boldsymbol{y}_i^T\boldsymbol{x}_{u} +\lambda \boldsymbol{x}_u = \sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i\]

\(\boldsymbol{x}_u\)를 \(\sum\) 밖으로 꺼냅니다.

\[\boldsymbol{x}_{u}\sum_{i}c_{ui}\boldsymbol{y}_i\boldsymbol{y}_i^T +\lambda \boldsymbol{x}_u = \sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i\]

좌항을 \(\boldsymbol{x}_u\)로 묶습니다.

\[(\sum_{i}c_{ui}\boldsymbol{y}_i\boldsymbol{y}_i^T +\lambda I) \boldsymbol{x}_u = \sum_{i}c_{ui}p_{ui}\boldsymbol{y}_i\]

해당 수식을 행렬 notation으로 표현하면,

\[(\boldsymbol{Y}\boldsymbol{C}^u\boldsymbol{Y}+\lambda I)\boldsymbol{x}_u = \boldsymbol{Y}^T\boldsymbol{C}^u\boldsymbol{P}(u)\]

이제 마지막으로 양변에 \((\boldsymbol{Y}^T\boldsymbol{C}^u\boldsymbol{Y} + \lambda I)^{-1}\)을 곱해주면 solution을 얻을 수 있습니다.

\[\boldsymbol{x}_u = (\boldsymbol{Y}^T\boldsymbol{C}^u\boldsymbol{Y} + \lambda I)^{-1} \boldsymbol{Y}^T \boldsymbol{C}^u \boldsymbol{P}(u)\]

'Collaborative Filtering for Implicit Feedback Datasets(ALS)' 논문 리뷰

Introduction

Characteristic of implicit data

Objective

Latent factor collaborative filtering

Notations

Our model

preference

confidence level

ALS

맺으며

Appendix

Step1. \(L\)을 \(\boldsymbol{x}_u\)로 편미분한 값을 구해봅시다.

Step2. 편미분 값을 0으로 놓고 수식을 전개

Reference

Trending Tags

'Collaborative Filtering for Implicit Feedback Datasets(ALS)' 논문 리뷰

Introduction

Characteristic of implicit data

Objective

Latent factor collaborative filtering

Notations

Our model

preference

confidence level

ALS

맺으며

Appendix

Step1. \(L\)을 \(\boldsymbol{x}_u\)로 편미분한 값을 구해봅시다.

Step2. 편미분 값을 0으로 놓고 수식을 전개

Reference

Further Reading

Enriching Word Vectors with Subword Information

Attention Is All You Need

Deep Learning is Robust to Massive Label Noise

Trending Tags