배치 정규화(batch normalization) 기법을 자주 활용했으나, 정확한 작동 원리에 대해서 알지 못했기 때문에 논문을 읽고 내용을 정리해 보았습니다. 친절한 논문은 아니어서 읽는데 꽤 시간이 걸렸습니다. 또한 관련 자료를 탐색 하던 중 배치 정규화 논문에서 주장하는 covariate shift에 대해 반박하는 논문도 있다는 정보를 보았는데요. 이 논문도 따로 정리해 보겠습니다. 먼저 논문의 내용을 요약하면 다음과 같습니다.
- 뉴럴넷 학습을 방해하는 요소로 Internal Covariate Shift 현상을 지목합니다. 다시 말해 학습이 진행되는 동안 network parameter들이 변화하면서 network activation의 distribution이 변화하기 때문에 뉴럴넷의 학습이 느려진다는 것입니다.
- 배치 정규화는 각 레이어의 출력값을 평균 0, 분산 1의 표준정규분포로 변환하기 때문에 covariate shift 문제를 벗어날 수 있습니다.
- 배치 정규화를 적용하면 다음의 이점을 얻을 수 있습니다.
- 학습률을 크게 셋팅할 수 있기 때문에 배치 정규화를 적용하지 않았을 때 대비 수렴 속도가 빠릅니다. 따라서 학습률 감소(learning rate decay)를 기존 보다 빠르게 가져갈 수 있습니다.
- randomness를 주기 때문에 regularization 효과가 있습니다. 따라서 드롭 아웃을 제거 할 수 있으며, 오버 피팅이 방지되는 효과가 있습니다.
1 Introduction
각 레이어의 인풋은 모든 이전 레이어의 파라미터(저자는 가중치라는 표현 대신 파라미터라는 표현을 사용합니다)에 영향을 받습니다. 따라서 앞선 레이어 파라미터의 작은 변화는 네트워크의 층이 깊어질수록 증폭될 것입니다. 각 레이어들은 이전 레이어의 출력 분포의 변화에 맞춰서 계속 해서 학습을 이어나가야 하기 때문에 이전 레이어의 출력 분포의 변화는 네트워크의 학습을 방해합니다.
저자는 이러한 현상을 internal covariate shift라고 부릅니다. 만일 각 출력층의 분포를 일정하게 유지할 수 있다면 covariate shift 현상을 억제하여 각 레이어가 이전 레이어의 출력 분포의 변화에 재적응(readjust)할 필요가 없으므로 학습을 원할하게 진행시킬 수 있을 것입니다.
레이어 출력 분포를 일정하게 유지시키는 것은 gradient를 잘 흐를 수 있게 한다는 이점도 있습니다. 시그모이드 활성화 함수 \(g(x) = \cfrac {1} {1 + exp(-x)}\)를 생각해 보죠. \(\vert x \vert\) 값이 커지면 그때의 gradient는 거의 0에 수렴하게 됩니다. 따라서 vanish graident 문제는 학습을 느리게 하는 주요 원인 입니다.
\(\vert x \vert\)값이 커지면 그때의 미분계수는 0에 가까워짐을 알 수 있습니다.
따라서 저자는 배치 정규화 기법(batch normalization)의 도입이 네트워크의 각 레이어의 출력 분포를 일정하게 만들어서 네트워크를 빠르게 수렴시킬 수 있다고 주장합니다. 배치 정규화는 네트워크 각 레이어의 출력 분포를 일정하게 유지하여 internal covariate shift 문제를 완화시켜 딥 뉴럴넷의 학습을 가속화시킵니다. 배치 정규화의 자세한 과정은 뒤에서 다시 언급하도록 하겠습니다. 이제 좀더 자세히 알아 보도록 하죠 👊
2 Towards Reducing Internal Covariate Shift
본 섹션에서 저자는 covariate shift를 줄이기 위해 필요한
먼저 internal covariate shift를 정확히 정의해야하겠습니다. internal covariate shift는 학습이 진행되는 동안 네트워크의 파라미터가 지속적으로 갱신됨에 따라 발생하는 네트워크 각 레이어의 출력 분포의 변화를 뜻합니다. 뉴럴넷 학습 과정에서 whitening을 통해 분포를 고정(fixing)하는 것은 학습의 수렴을 빠르게 한다는 것이 기존 연구에 의해 알려져 있습니다([2]). activation을 whitening 하는 방법은 다양합니다. 하지만 중요한 점은 whitening 과정이 반드시 gradient descent 과정에 포함되어야 한다는 것입니다. 그렇지 않다면 어떻게 될까요? 예를 들어 input \(u\)와 learnable bias \(b\)를 더한후 normalization을 진행하여 \(\hat x\)을 출력하는 간단한 네트워크를 생각해봅시다.
\[\hat x = x - E[x],\] \[\text {where} \space x=u+b, \space X=\{x_{1 ...N}\} \space \text{is the set of values of} \space x \space \text{over the training set}, \space \text{and} \space E[x] = \frac{1}{N} \textstyle \sum_{i=1}^{N}x_{i}\]만일 gradient descent 과정에서 \(E[x]\)의 \(b\)에 대한 의존성을 고려하지 않고 계산 된다면 어떻게 될까요? \(E(X)\) 방향으로 gradient를 흘려 보내 않을 때의 상황을 생각하면 직관적으로 이해가 됩니다. 아래의 그림에서 ❌ 부분에 gradient가 흐르지 않는다고 생각해보세요.
\(\Delta b\)는 \(\frac{\partial l}{\partial \hat x}\)에 비례하게 됩니다.
epoch가 한번 돌면 \(b\)는 \(b+\Delta{b}\)로 업데이트 됩니다.
따라서 새로운 \(\hat{x}\)는 아래와 같이 계산 됩니다.
\[\begin{aligned} \hat{x} &= u+(b+\Delta{b}) - E[u+(b+\Delta{b})] \\ &= u+b+\Delta{b}-E[u+b]-\Delta{b} \\ &= u+b - E[u+b] \\ &= x-E[x] \end{aligned}\]
분명히 \(b\)를 업데이트 했는데도 불구하고 \(\hat{x}\)의 값이 업데이트 전과 동일합니다. 이렇게 되면 파라미터 \(b\)가 발산해 버리게 됩니다. 왜냐하면 \(b\)는 \(\Delta{b}\)만큼 계속 해서 그 값이 커지는데, \(\hat{x}\) 값은 학습을 아무리 진행해도 특정 값으로 고정되기 때문입니다. \(\Delta{b}\)는 \(\frac{\partial l}{\partial \hat{x}}\)에 비례하는데, 계산 그래프 상에서 \(b\)를 제외한 모든 값이 고정적이기 때문에 \(\Delta{b}\)는 일정하게 계속 증가되어 결국 발산해버리는 것이죠. 저자는 초기 실험에서 이러한 상황을 경험적으로 확인하였으며, loss에 대한 gradient를 구할 때 normalization 과정도 함께 고려함으로써 문제를 해결했다고 합니다.
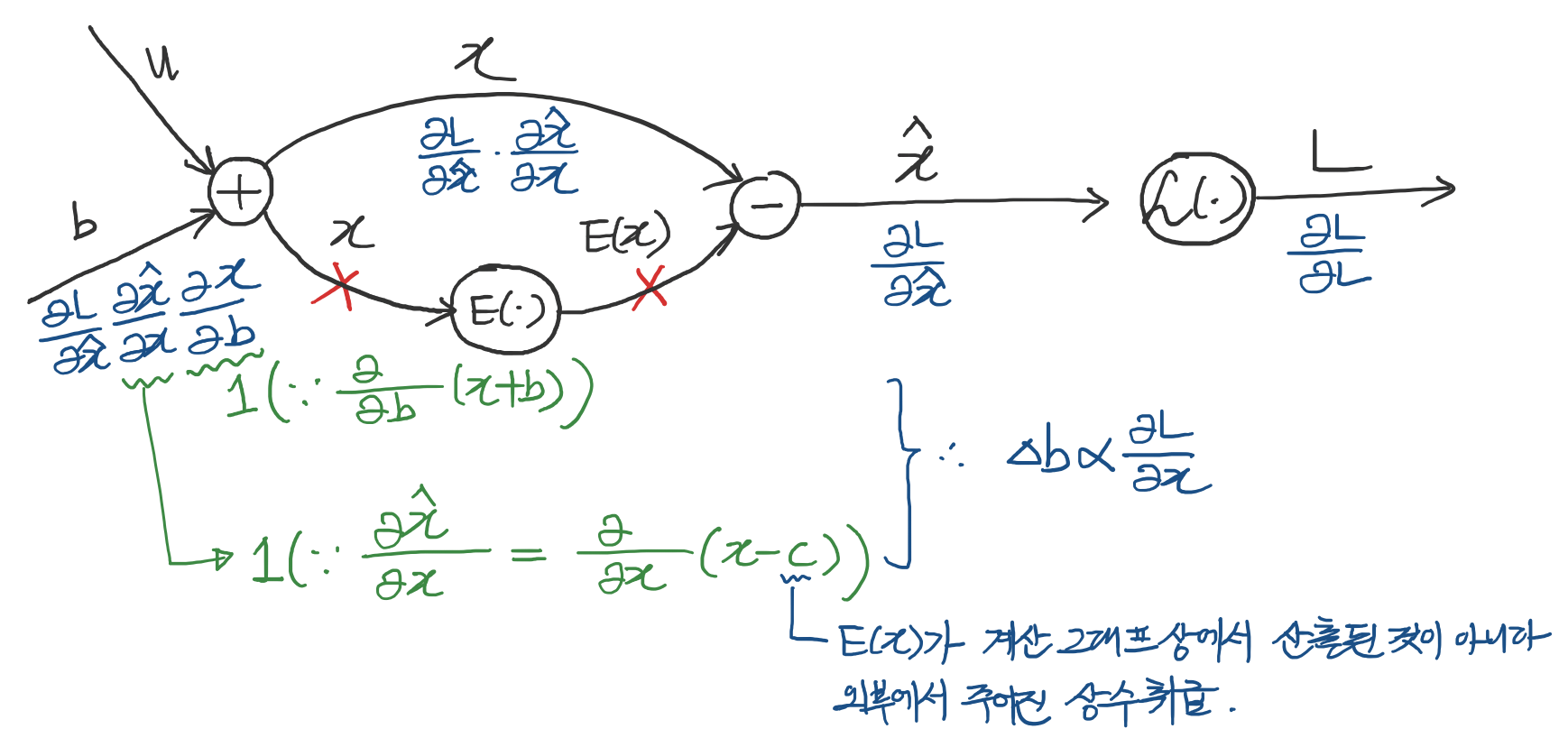간단한 레이어의 계산 그래프. \(E(x)\)의 \(b\)에 대한 의존성을 고려하지 않으면 학습 과정상에 문제가 발생하게 됩니다.
이제는 사고를 한차원 확장하여 \(x\)를 vector로 생각하고 \(X\)를 이러한 vector들의 set으로 생각해봅시다. \(x\)는 \(u\)와 \(b\)를 곱한 값이라는 점을 주의해주세요. 이러한 셋팅에서 \(\hat{x}\)를 구하는 과정을 다음과 같이 단순할 수 있습니다.
\[\hat{x} = Norm(x, X)\]\(\hat{x}\)는 개별 example인 \(x\)뿐만 아니라 전체 데이터셋 \(X\)에도 의존한다는 것을 알 수 있습니다. 또한 역전파를 위해서는 다음과 같은 자코비안 행렬을 계산해야 합니다.
\[\cfrac{\partial \text{Norm}(x, X)}{\partial x} \space \text{and} \space \cfrac{\text{Norm}(x, X)}{\partial X}\]위 식에서 두번째 term을 무시하게 되면 앞서 언급한 \(b\)의 발산 문제가 똑같이 발생하게 됩니다. 왜 두번째 term과 앞서 언급한 현상이 관련이 있다는 것일까요? 충분히 고민하다가 내린 개인적인 생각을 덧붙여보겠습니다. 전체 데이터셋이 2개인 상황을 가정해보면 normalization 계산 그래프는 아래의 figure처럼 표현 할 수 있습니다. \(b\)가 발산하는 문제는 \(E(x)\)쪽 경로의 gradient를 고려하지 않았을 때 발생한다는 점을 앞서 언급하였습니다. 그런데 \(E(x)\)를 구하는 과정에서 전체 데이터셋 \(X\)가 필요하게 됩니다. 데이터셋이 2개인 상황을 가정하였으므로 \(X=\{x_{1}, x_{2}\}\)라고 생각할 수 있겠네요. 결국 위 식에서 말하는 전체 데이터 셋에 대한 미분값은 \(E(x)\) 쪽 경로로 흘러가는 gradient라고 생각할 수 있습니다.
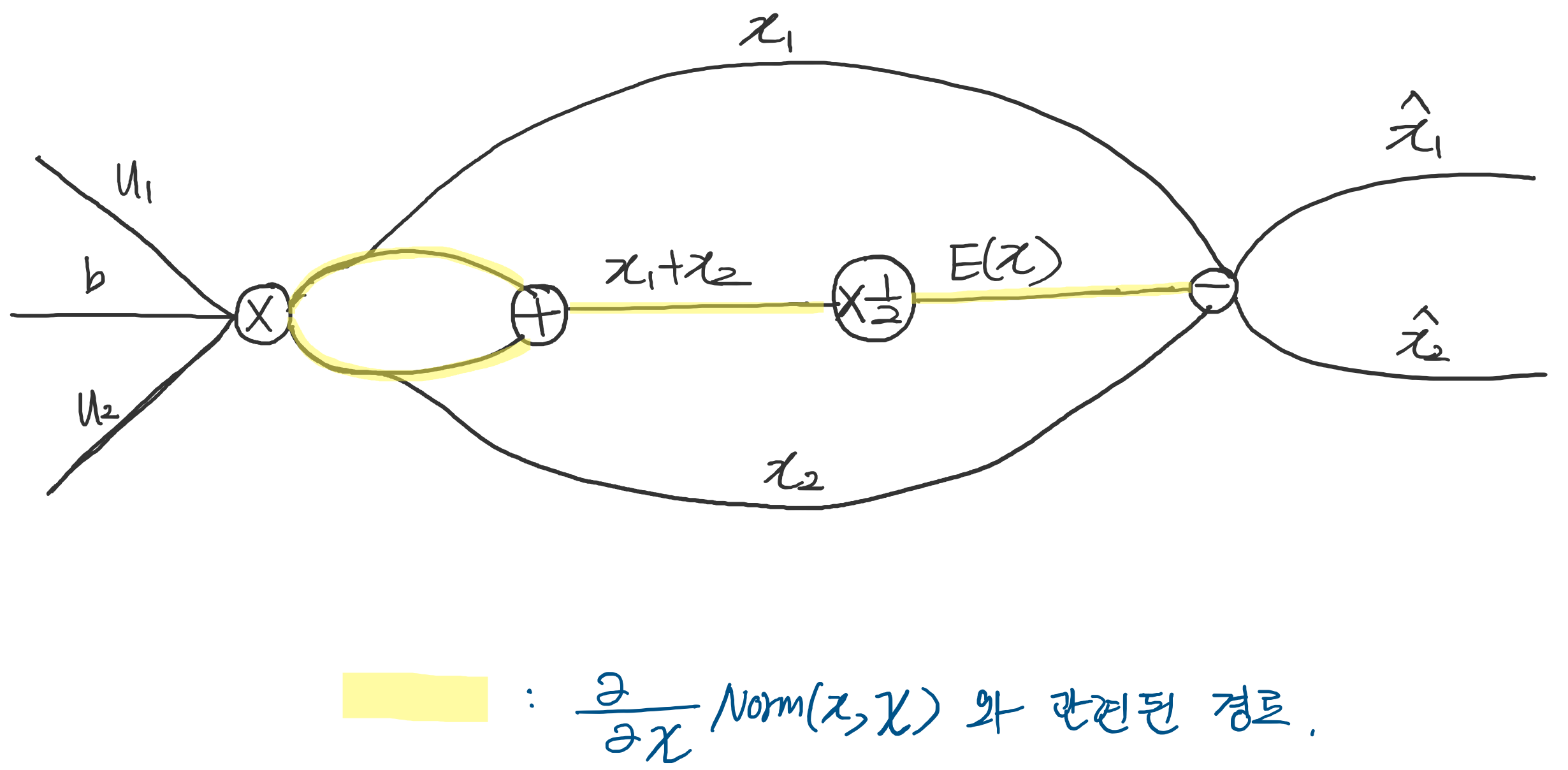
다시 논점으로 돌아와서, 이러한 셋팅에서 normalization을 진행하기 위해서는 다음과 같은 공분산 행렬과 그것의 inverse square root에 대한 연산이 필요하며 해당 연산들에 대한 미분값 역시 필요하게 됩니다. normalization 과정에 엄청난 연산이 요구되는 것이죠.
\[\text{Cov}[x] = E_{x \in X}[xx^T] - E[x]E[x]^T \space \text{and} \space \text{Cov}[x]^{-1/2}(x-E[x])\]따라서 저자는 1) 미분 가능하면서(gradient descent 과정에 포함시키기 위해) 2) 전체 트레이닝 셋을 고려하지 않는 normalization기법을 고안하게 됩니다. 바로 배치 정규화 기법이죠!
3 Normalization via MIni-Batch Statistics
앞서 언급했다시피 full whitening은 매우 계산량이 높고, 모든 곳에서 미분이 가능하지 않다는 단점이 있습니다. 따라서 저자는 각각의 feature들을 독립적으로 zero mean and unit variance로 만드는 방법을 제안합니다. 이러한 normalization 방식은 feature 간 decorrelated가 되지 않았을 때도 모델의 수렴 속도를 빠르게 만든다는 것이 기존 연구에서 입증되었습니다(LeCun et al., 1998).
4 Experiments
5 Conclusion
Reference
Papers
Articles
배치 정규화 논문 리뷰 (Batch normalization) - Slow walking manhttps://arxiv.org/abs/1404.5997)