최근 사내에서 CS50 스터디를 시작했습니다. 본 포스팅은 CS50의 첫번째 주제인 ‘컴퓨팅 사고’의 내용을 정리합니다. 컴퓨터는 정보를 어떤 방식으로 표현할까요? 그리고 컴퓨터는 정보를 어떻게 처리할까요? 오리엔테이션 성격의 강의이기 때문에 가볍게 정리해보려고 합니다.
본 포스팅에서는 다음의 내용을 다룹니다.
- 컴퓨터가 ‘숫자’를 이해하는 방법
- 컴퓨터가 ‘문자’를 이해하는 방법
- 알고리즘
컴퓨터가 숫자를 이해하는 방법
10진법
컴퓨터는 0과 1만 이해할 수 있다는 이야기를 많이 들어 보셨을 겁니다. 그런데 우리는 너무나 당연하게도 컴퓨터로 아주 큰 수를 다룰 수도 있고, 문자를 활용하여 문서도 작성하고 유튜브 영상도 보고 음악 감상도 합니다. 겨우 0과 1 두 가지 숫자만 처리할 수 있는데 이렇게 복잡한 정보를 어떻게 처리하는 걸까요?
컴퓨터가 숫자를 다루는 방법부터 시작하는게 좋겠습니다. 서두에서 언급했다시피 우리가 일상생활에서 사용하는 컴퓨터는 0과 1, 이 두 가지 숫자만 이해할 수 있습니다. 하지만 0과 1만 있으면 우리가 알고 있고 + 상상할 수 있는 모든 수를 표현할 수 있습니다. 이게 어떻게 가능할까요? 우리는 10진법을 사용하는데 매우 익숙합니다. \(13\), \(535\), \(46357\) 등 일상에서는 거의 모든 수를 십진법으로 표현하고 있죠. 특히 \(13\)이라는 숫자를 다음과 같이 표현할 수 있다는 사실도 당연하게 받아들일 수 있습니다.
\(13\)은 \(10^1\)자리수와 \(10^0\)의 자리수로 분리해서 생각해볼 수 있습니다. 중요한 점은 십진법에서는 숫자를 \(10\)의 거듭제곱으로 표현하고 있다는 것입니다. 그리고 \(10^1\) 자리수인 1과 \(10^0\) 자리수인 3을 이어 붙여서 \(13\) 이라는 숫자로 나타냅니다. 이 것이 숫자를 10진법의 시스템에서 표현하는 방법입니다. 10진법은 숫자를 0~9를 활용해서 표현합니다.
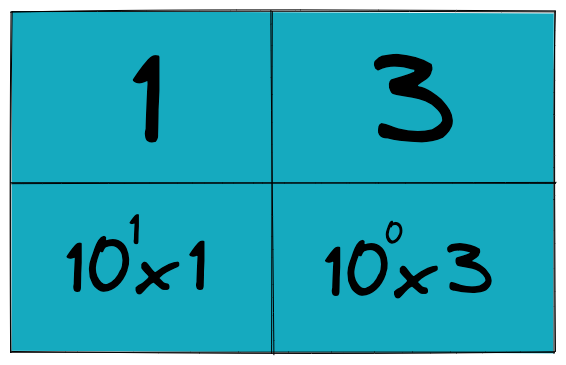
2진법
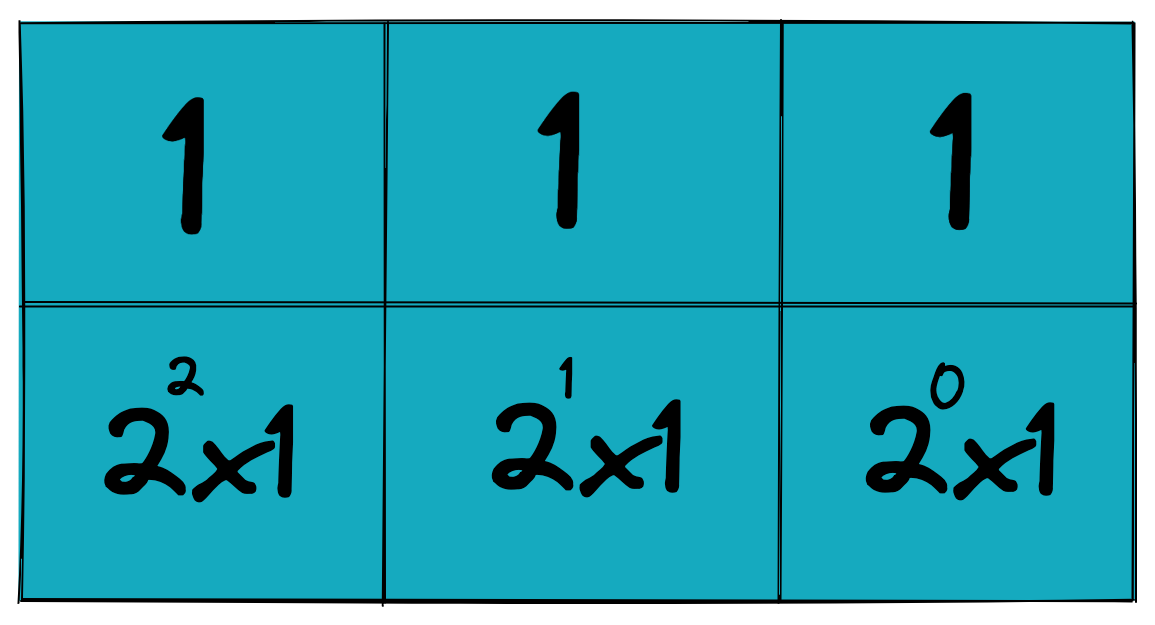
컴퓨터는 0과 1만을 이용해서 모든 연산을 처리합니다. 다시 말해, 2진법으로 수를 표현하는 것이죠. 10진법은 숫자를 10의 거듭제곱으로 표현하는 것과 같은 원리로 2진법에서는 숫자를 2의 거듭제곱으로 표현합니다. 십진수 13을 2의 거듭제곱으로 표현하면 다음과 같습니다.
그리고 \(2^3\) 자리수 1, \(2^2\) 자리수 1, \(2^0\) 자리수 1을 이어 붙이면 \(111\)이라는 수가 나타납니다. 즉 십진법 13은 이진법 111로 표현되는 것이죠. 두 수는 수의 시스템이 다를 뿐 완벽하게 같은 숫자입니다. 따라서 우리가 10진법으로 생각하는 모든 수는 2진법으로 표현할 수 있습니다. 따라서 컴퓨터는 0과 1만 이용하더라도 매우 큰 수를 표현할 수 있게 되는 것이죠.
왜 하필 2진법을 사용할까?
그렇다면 왜 컴퓨터는 왜 2진법을 사용할까요? 컴퓨터에서 연산을 담당하는 CPU는 수많은 트랜지스터로 구성되어 있습니다. 이 트랜지스터는 전기 신호를 받았을 때 일정 기준 이상의 전압이 걸리면 전기 신호를 출력(1)하고 그렇지 않으면 전기 신호를 출력하지 않는(0) 식으로 설계 되어 있습니다. 컴퓨터의 언어가 2진법인 것은 트랜지스터의 작동 원리에 기인한 것이라고 할 수 있습니다.
하지만 2진법은 인간의 입장에서 보면 좀 불편한 것이 사실입니다. 일상에서 흔히 접할 수 있는 시스템이 아니기 때문인데요. N진법을 사용하면 하나의 트랜지스터에서 표현할 수 있는 정보의 양이 더 많아지기 때문에 훨씬 좋을 것 같은데, 왜 기술이 발달한 지금까지도 2진법 시스템을 고수하고 있을까요?
먼저 2진법 만으로도 인간의 모든 논리 연산을 표현할 수 있기 때문입니다. CPU는 수많은 트랜지스터로 구성되어 있다고 했습니다. 트랜지스터 하나는 0 또는 1, 즉 2가지 정보만 표현이 가능합니다. 하지만 수많은 트랜지스터의 출력값을 조합하면 더 풍성한 정보를 표현할 수 있고 논리 연산(AND, OR, XOR 등), 사칙 연산 등이 충분히 가능합니다. 2진법만으로도 정보의 표현력에 한계는 없는 것이죠.
그리고 2진법은 N진법에 비해서 오류가 최소화되고 시간 효율성에서 합리적입니다. 트랜지스터는 특정 전압을 임계값으로 하여 전기 신호를 출력(1) 할지 말지(0)를 결정한다고 하였는데요. 만일 N진법을 사용한다면 전압을 좀더 세밀한 단위로 나누어서 구분해야 할 것입니다. 따라서 전압을 좀 더 정확하게 측정하는데 드는 시간 비용이 발생하게 됩니다. 또한 외부의 노이즈에 영향을 받을 수도 있죠. 결과적으로 0과 1로 단순하게 구분하는 것이 훨씬 효율적인 방법이라고 할 수 있습니다 (Simple Is Best!).
컴퓨터가 문자를 이해하는 방법
컴퓨터가 2진수를 활용하여 숫자를 표현한다는 사실은 알게 되었습니다. 그런데 숫자보다 훨씬 복잡한 문자는 컴퓨터가 어떻게 표현하고 이해할까요? 결론부터 말하면 컴퓨터에서 다루는 모든 정보는 0과 1로 이루어진 bit로 표현합니다. 이는 문자도 예외가 아닙니다. 문자를 이진수로 변환하는 것을 문자 인코딩(encoding)이라고 하고, 이진수를 인간이 이해할 수 있는 문자로 변환화는 과정을 디코딩(decoding)이라고 합니다.
문자열을 인코딩하는 방식은 다양한데요. 대표적으로 ASCII와 Unicode를 들 수 있습니다. 이에 대한 더 자세한 설명은 여기를 참조해주세요.
ASCII(American Standard Code for Information Interchange)
ASCII는 문자를 7bit로 표현하는 표준문자체계입니다. 따라서 ASCII는 \(2^7=128\)개의 문자만 표현할 수 있는데, 이는 영문 키보드에서 사용할 수 있는 모든 문자를 표현할 수 있는 수준입니다. 그러나 표현해야하는 문자가 점차 증가함에 따라 7bit로 문자를 표현하는 것에 한계가 드러났습니다. 이후에 8bit(1byte)를 쓰는 확장 ASCII가 등장했습니다. 확장 ASCII는 기존 ASCII에 비해 2배 많은 문자를 표현할 수 있습니다.
Unicode
유니코드는 전 세계의 모든 문자를 일관되게 표현할 수 있는 표준문자체계입니다. ASCII는 전 세계의 다양한 문자를 담지 못합니다. 이에 따라 다양한 문자를 담을 표준이 필요해졌는데, 이에 따라 유니코드가 등장하게 되었습니다. 유니코드는 문자를 2~4btye 숫자 (코드 포인트)로 1:1 맵핑을 해 놓은 문자 집합(character set)입니다. 헷갈릴만한 점은 유니코드는 ASCII와 다르게 특정 인코딩 방식을 가르키는 것은 아니라는 것입니다. UTF-8, UTF-16, UTF-32과 같은 용어를 들어 보셨을 텐데요. 이들이 바로 유니코드를 활용한 인코딩 방식입니다.
알고리즘
알고리즘이란?
지금까지 컴퓨터가 정보를 표현하는 방법을 알아보았습니다. 그렇다면 컴퓨터는 정보를 어떻게 가공해서 출력할까요? 컴퓨터가 정보를 처리하는 단계적인 방법을 알고리즘이라고 합니다. 알고리즘이란 멀리 있는 것이 아닙니다. 인간의 사고 과정도 결국엔 알고리즘입니다.
전화번호부에서 mike smith를 찾아보자.
512 페이지짜리 전화번호부에서 mike smith의 전화번호를 찾는 문제가 주어졌다고 가정해봅시다. 그리고 이 전화번호부는 알파벳 순으로 정렬되어 있습니다. 이 문제를 어떻게 풀어볼까요?
먼저 가장 단순하게는 첫페이지부터 차례 차례 mike smith를 찾는 것입니다. 1 페이지 2 페이지 … 최악의 경우에는 512 페이지까지 다 보아야만 mike smith를 발견할 수도 있습니다. 이러한 탐색 방법을 선형 탐색이라고 합니다. 선형 탐색은 매우 정확한 방법이지만 동시에 매우 비효율적인 방법임을 짐작하실 수 있을 겁니다.
더 효율적인 방법이 있을까요? 먼저 전체의 절반인 256 페이지를 펴 봅니다. mike smith가 있으면 탐색을 종료해도 됩니다. 그러나 없다면, 우리는 mike smith가 256 페이지보다 앞에 있을지 뒤에 있을지 알 수 있습니다. 만약 mike smith가 256 페이지보다 이전에 있다면 이후의 페이지들은 더 이상 탐색할 필요가 없습니다. 이러한 과정을 반복 진행하면 처음부터 차례로 탐색하는 방법 보다는 훨씬 효율적으로 탐색할 수 있습니다. 물론 정확성도 보장되구요. mike smith가 64 페이지에 있었다면 3번만 탐색해도 정확하게 찾을 수 있습니다. 이러한 탐색 방법을 분할 정복이라고 합니다.
컴퓨도로 방금 예시의 알고리즘을 그대로 구현할 수 있습니다. 다음의 구성 요소를 통해서요.
- function
- condition
- boolean expressions
- loops
- variables
- …
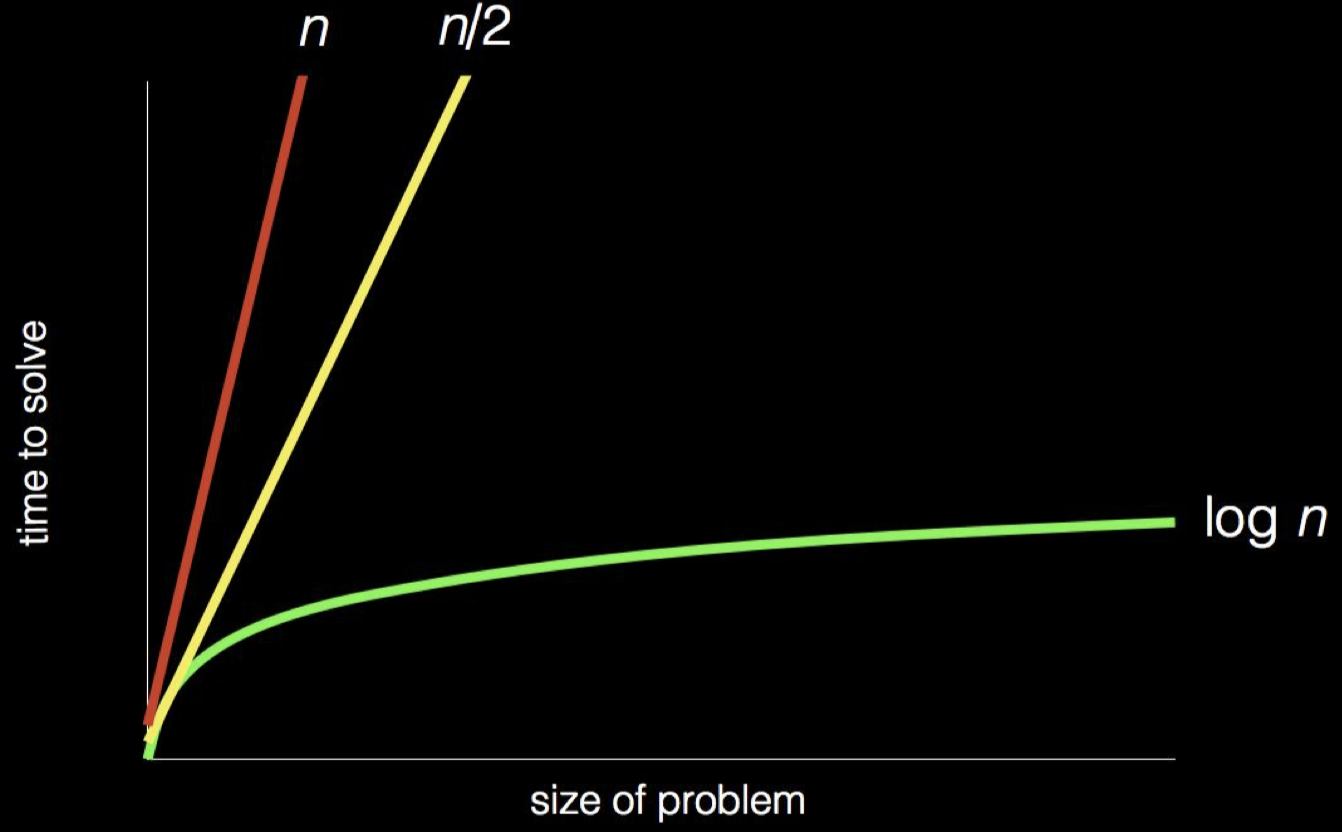
더 효율적인 알고리즘?
전화번호부의 예시에서 처럼 같은 문제를 해결하더라도 더 효율적인 알고리즘이 존재합니다. 같은 양의 데이터가 인풋 되었을 때, 문제를 해결하는데 시간이 덜 걸리는 알고리즘이 더 효율적인 알고리즘입니다. 강의 후반부에 정렬 알고리즘을 배우면서 이 부분은 더 자세히 다룰 기회가 있을 것 같습니다.