현업의 데이터를 다루다보면 데이터에 noisy label이 많이 발생합니다. 가장 좋은 점은 일일이 수작업으로 data cleaning을 하는 것이 좋겠지만, 데이터의 양이 늘어남에 따라 라벨링을 교정하는 것 자체가 일이 되는 경우가 발생하게 됩니다. 이와 관련된 고민을 하던 중 noisy label이 모델에 끼치는 영향력을 분석한 논문을 발견하여 읽고 리뷰해보도록 하겠습니다. 먼저 이 논문의 결론을 정리하자면 다음과 같습니다.
- 충분히 큰 클린 데이터셋이 구축되어 있으면, 노이즈 데이터로 인한 악영향을 극복할 수 있습니다.
- noisy data가 증가함에 따라 필요한 clean data의 개수는 선형적으로 증가하는 경향이 있습니다.
- 배치 사이즈를 크게 하거나 학습률을 작게 하면 노이즈 데이터로 인한 performance 손실을 완화할 수 있습니다.
- 비록 딥뉴널넷은 noisy 데이터에 robust한 면을 보이지만, 같은 양의 학습 데이터안에서 clean data의 비중이 높을 수록 performance가 좋습니다.
1 Learning with massive label noise
본 논문에서는 클린 데이터의 크기는 고정한 상태에서 noisy 데이터의 크기를 점차 늘려감에 따라 multi-class classification task의 성능을 평가하는 방법을 통해 noisy data로 인한 결과를 보고자 하였습니다. clean data의 크기를 \(n\), 클린 데이터 당 noisy 데이터의 개수를 \(\alpha\)라고 하였습니다. 따라서 최종적인 데이터 셋의 크기는 \(n+\alpha n\)가 됩니다. 본 논문에서는 \(\alpha\)의 크기를 변화시켜감에 따라 performance가 어떻게 변화하는지를 체크합니다. 특히 label noise를 아래의 3가지 유형으로 분류하여 실험을 진행했다는 점이 흥미롭네요.
- uniform label-swapping
- structured label-swapping
- out-of-vocabulary examples
1.1 Training with uniform label noise
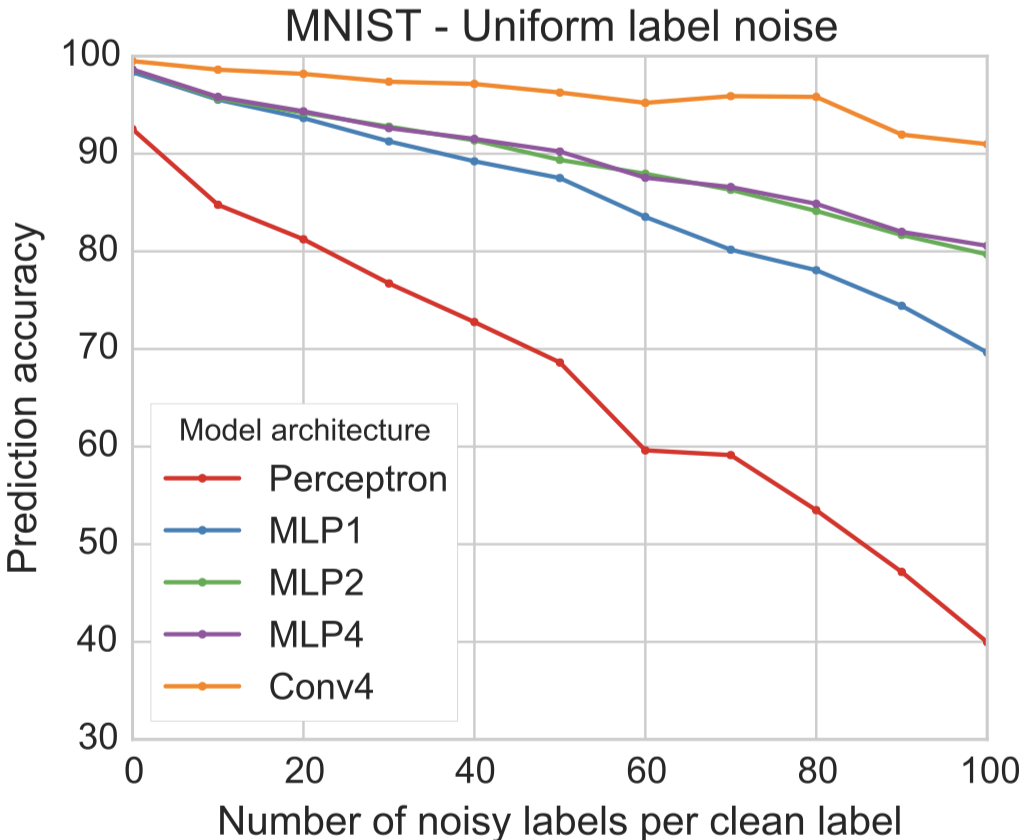
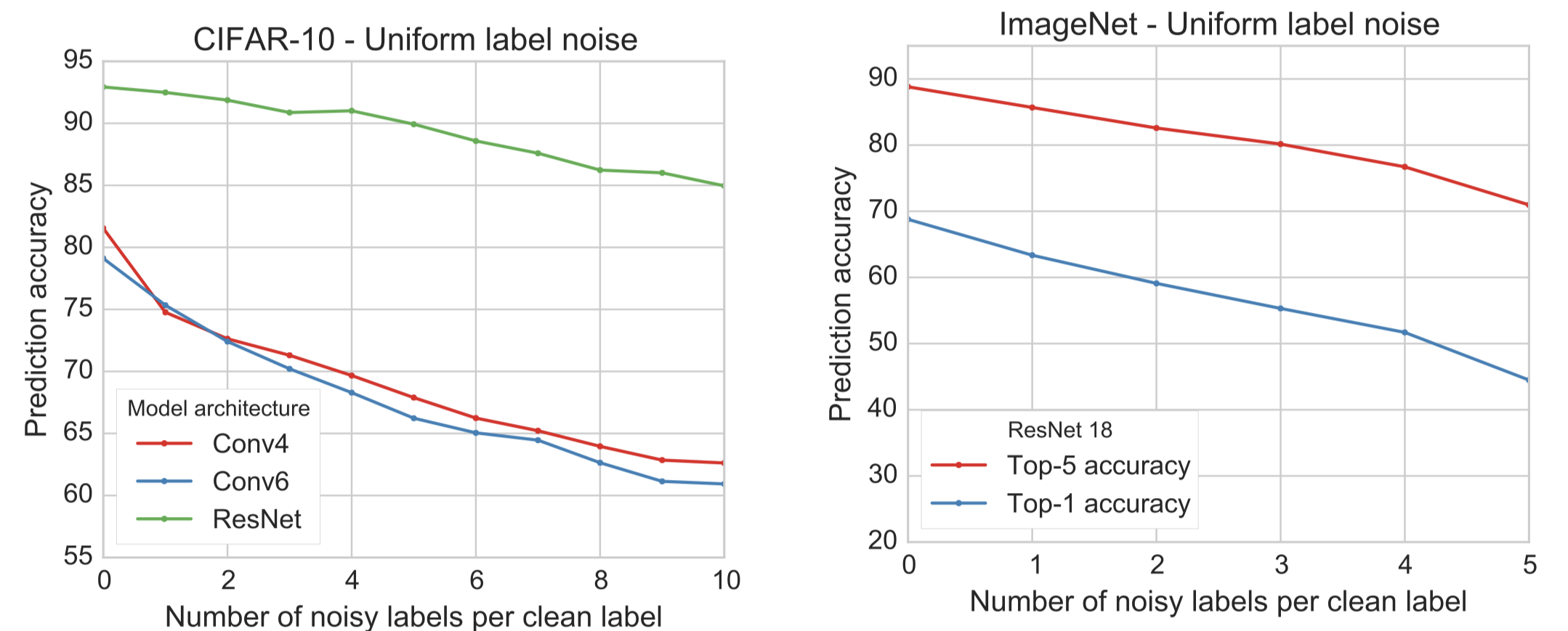
첫번재 실험은 noisy label data가 correct label data가 보다 많은 일반적인 상황을 보여줍니다. 이때 생성되는 noisy data에 붙일 label은 uniform distribution에서 뽑습니다. 다시 말해 모든 label이 같은 확률로 추출될 수 있다는 것입니다. 예를 들어 \(n=5\)이고 \(\alpha = 10\)이면 noisy data를 총 50개를 생성해야하는데, 그 50개 data에 대한 uncorrect label은 어떤 label이든 동일한 확률 설정된다는 것입니다. 아래의 figure를 보고 결과를 봅시다. 다음의 경향이 있음을 할 수 있습니다.
- noisy data per clean label의 개수가 증가함에 따라 test performance가 감소하는 경향이 있습니다.
- network architecture가 클수록 label noise에 robust한 경향이 있습니다.
- noise tolerance가 필요한 분야일 수록 ConvNets이나 RestNets 등의 깊은 구조가 필요합니다.
1.2 Training with structured label noise
뉴럴넷은 uniform label noise에 robust 하다는 것을 보였습니다. 그러나 일반적인 실무 환경에서 수집된 데이터의 경우, 노이즈 데이터의 확률 분포가 uniform distribution을 따르는 비현실적입니다. 따라서 두번째 실험에서는 현업에서의 현실성을 좀 더 반영하기 위해 noisy label의 분포를 특정한 noisy label structure를 통해 실험을 진행하였습니다. 특히 3가지의 noisy label structure를 실험하였습니다.
먼저 correct label을 뽑을 확률 \(\varepsilon=1/(1+\alpha)\)를 정의하고, noisy label의 structure를 유도하기 위해, noisy label 중 특정 클래스가 뽑일 확률에 bias를 주는 방법을 취했습니다. 이를 위해 \(\delta\)라는 파라미터를 간단하게 도입하였는데요. \(\delta\)는 noisy label의 structure의 정도를 표현합니다. 저자는 이를(\(\delta\))를 샘플링 될 가능성이 두번째로 높은 클래스의 가능성의 정도가 우연을 넘어설 정도(over chance)라고 정의합니다. 직역 하면 말이 어려운데, 여기서 말하는 ‘우연’은 uniform structure를 뜻합니다. uniform structure는 모든 라벨이 샘플링될 확률이 동일합니다. 바꿔 말하면, 모든 라벨이 샘플링될 확률이 우연(랜덤)하다는 것이죠. 말로 풀어쓰는 것보다 figure로 보는 것이 더 이해하기 쉬우실 것 같습니다. 아래의 figure를 보시면 왼쪽은 uniform noise일때의 label의 strurcture(혹은 distribution이라고 표현해도 될 것 같습니다)이고 오른쪽은 structured noise에 대한 예시입니다. \(\delta\varepsilon\)라고 적힌 부분을 보시면 두번째로 가능성이 높은 클래스가 뽑힐 확률이 uniform noise(우연히) 대비 얼마나 높아졌느냐를 뜻한다는 것을 알 수 있습니다. 따라서 \(\delta=0\)이면 uniform noise와 완전히 동일하게 되고, \(\delta=1\)이면 두번째로 샘플링 될 확률이 높은 클래스의 가능성이 correct label의 확률과 동일하게 됩니다. 따라서 \(\delta\)를 0과 1사이의 값으로 조절하면 noise의 structure를 자유롭게 조절 할 수 있습니다. 참고로 다른 label의 likelihood는 linear하게 scale 한다고 언급되어 있습니다.
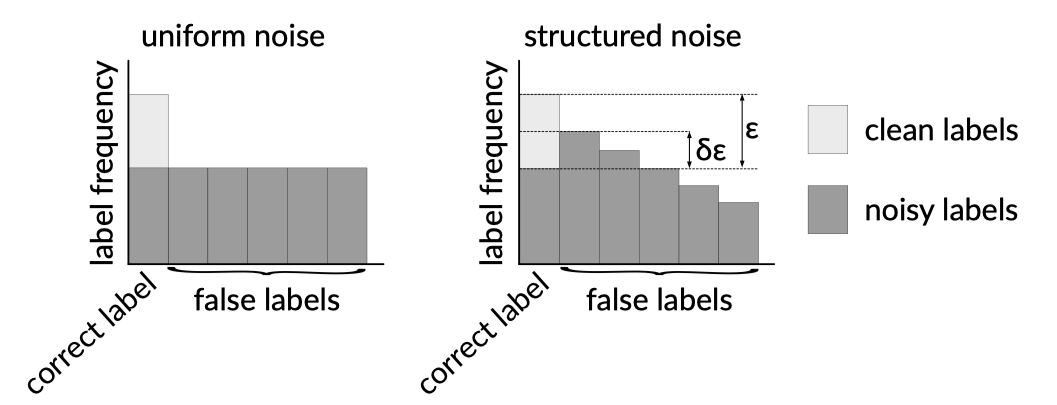
저자는 noise label을 3가지 유형으로 구분하여 실험을 진행하였습니다.
- labels biased towards hardly confused classes(Confusing order): correct label과 비교해서 헷갈리기 쉬운(confused) 라벨순으로 많이 뽑음
- labels biased towards easily confused classes(Reverse confusion order): correct label과 비교해서 헷갈리기 쉬운(confused) 라벨의 역순으로 많이 뽑음
- labels biased towards random classes(Random order): noise structure를 random으로 구성
그 결과는 아래와 같이 요약할 수 있습니다.
- 3가지 유형의 noise structure 간에 결과의 큰 차이가 없었습니다.
- \(\delta\)가 커질수록 모델의 정확도가 감소하는 경향이 있습니다.
- 이 결과는 현실적인 noisy dataset에서도 deep neural net이 좋은 결과를 보여주는 이유에 대해 설명해줄 수 있습니다.
1.3 Source of noisy labels
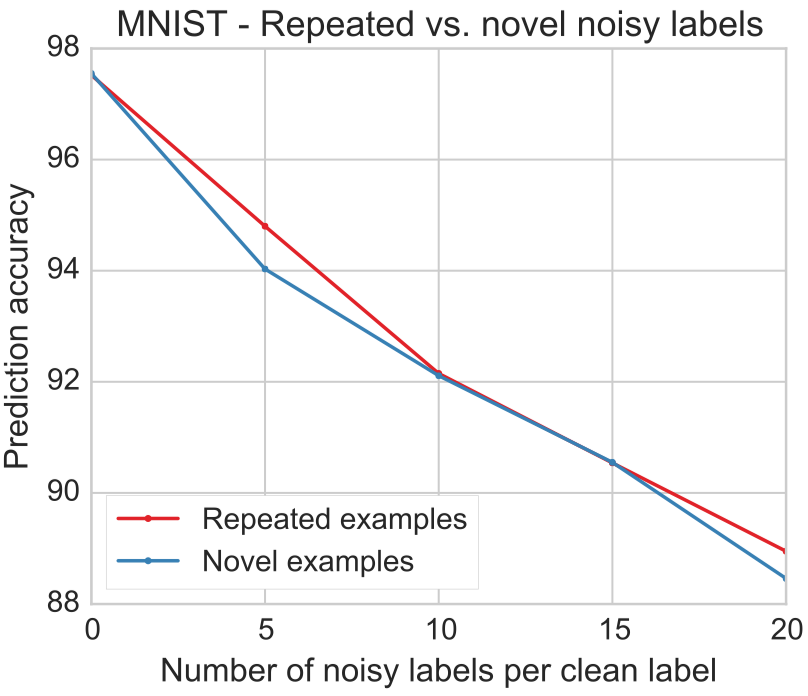
1.1~1.2의 실험들은 같은 dataset에서 뽑은 데이터에 false label을 할당하여 진행한 실험들이었습니다. 그러나 natural scenario에서는 noisy example들이 다른 data source에서 발생된 경우가 많습니다. 따라서 저자는 다른 data source에서 발생된 noisy example에 대한 실험도 필요하다고 언급합니다. 따라서 CIFAR10 데이터셋을 기준으로 두가지 실험을 진행하였습니다.
- Examples from similar but different dataset: CIFAR-10 데이터셋의 라벨을 기준으로 CIFAR-100 데이터에 noise label을 할당한 데이터를 사용
- Examples from simply white nosie: CIFAR-10 이미지 데이터 픽셀의 평균과 분산을 이용하여 random noise 생성하여 CIFAR-10 데이터의 라벨을 랜덤으로 할당
결과를 요약하면 다음과 같습니다.
- white noise example의 prediction accuracy가 가장 높습니다. 이는 neural net이 random noise에 fitting 할 수 있다는 기존의 연구 결과와 일치합니다(Zhang et al., 2017)
- 비슷(관련)하지만 다른 데이터셋에서 추출한 데이터가 같은 데이터셋에서 추출한 데이터보다 prediction accuracy가 높습니다.
논문에서는 결과를 위와 같이 언급하였는데, white noise example이 다른 noise example에 비해서 정확도가 높게 나온 것은 직관적으로 조금 이해하기 힘든 부분입니다. 저자는 해당 실험의 결과를 다음과 같이 해석합니다. 대부분의 noisy data는 CIFAR-10과 CIFAR-100 사이의 데이터(어느 정도 관련은 있지만, 데이터가 이곳저곳에 수집되었기 때문에 source가 다른)입니다. noisy data 중 일부는 관련도가 깊은 데이터이지만 mislabeld 되어서 학습에 부정적인 영향을 주겠지만, 대부분의 noisy data는 관련도가 현저히 떨어지기 때문에 학습에 부정적인 영향을 주지 못했기 때문입니다.
이 실험 결과에 제 생각을 덧붙여 보면, examples from similar but different dataset에 대한 실험은 noisy data를 만드는 과정에서 label을 랜덤하게 할당하기 때문에 큰 틀에서 보면 white noise 데이터로 실험한 것에 포함될 수 있다고 볼 수 있습니다. 그러나 examples from similar but different dataset는 원래의 데이터와 어느정도 관련성이 있는 반면에, white noise 데이터는 실제 데이터와 관련도가 상대적으로 매우 적기 때문에 학습 과정에 부정적인 영향을 주는 정도 훨씬 적을 것으로 생각해볼 수 있습니다. 따라서 오히려 white noise dataset의 prediction accuracy가 더 높게 나온 것 같습니다.
2 The importance of larger datasets
사실 이 부분이 논문에서 핵심적으로 주장하고 싶은 내용을 담은 부분이라고 볼 수 있습니다. 딥러닝에 큰 데이터셋이 필요하다는 것은 널리 알려진 사실입니다(Deng et al., 2009; Sun et al., 2017). 저자는 noisy example이 많은 데이터셋에서는 데이터셋의 크기가 어떤 영향을 미치는지를 알아보고자 하였습니다. 결과적으로 말씀드리면 저자는 다음의 내용을 주장합니다.
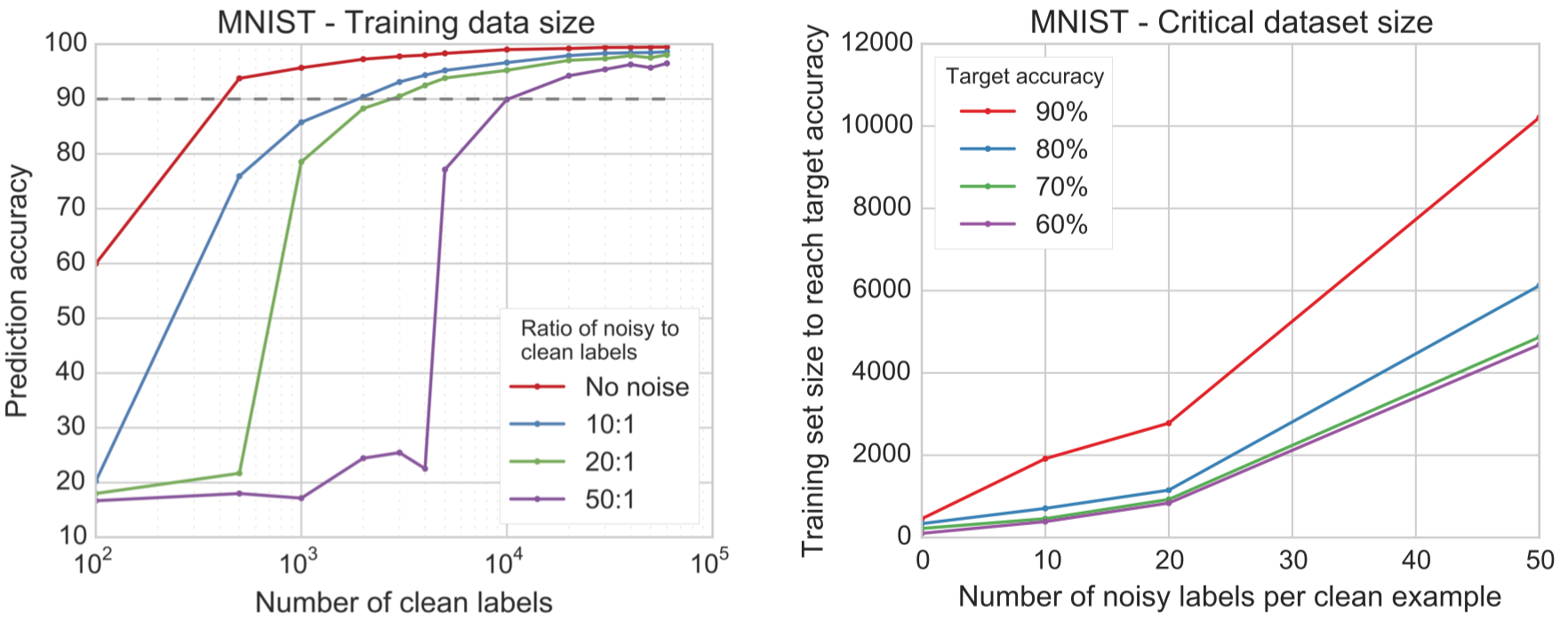
- 데이터셋 내에 noisy label data의 비중이 클수록 같은 accuracy에 도달하기 위해 필요한 clean data의 개수가 증가하는 경향이 있습니다.
- 데이터셋 내에 noisy label data의 비중에 따라 accuracy를 급격하게 증가시키는 threshold dataset의 크기가 다릅니다.
아래의 왼쪽 figure를 보면, noisy label:clean label의 비중이 50:1일 때가 20:1일 때보다 accuracy 90%를 달성하기 위해 필요한 clean label의 개수가 많음을 알 수 있습니다. 아래의 오른쪽 figure도 역시 일맥상통한 결과를 주장하고 있습니다.
3 The importance of batch size and learning rate
지금까지는 뉴럴넷 학습시 필요한 하이퍼파라미터를 일정한 값으로 고정시켜 실험을 진행하였습니다. 그러나 저자는 배치사이즈와 학습률이 gradient update의 stochasticity를 줄여주는 중요한 요소로 보고, 두 하이퍼파라미터 값의 변화에 따른 accuracy 스코어를 관찰하였습니다. 그 결과 다음의 결론을 주장합니다.
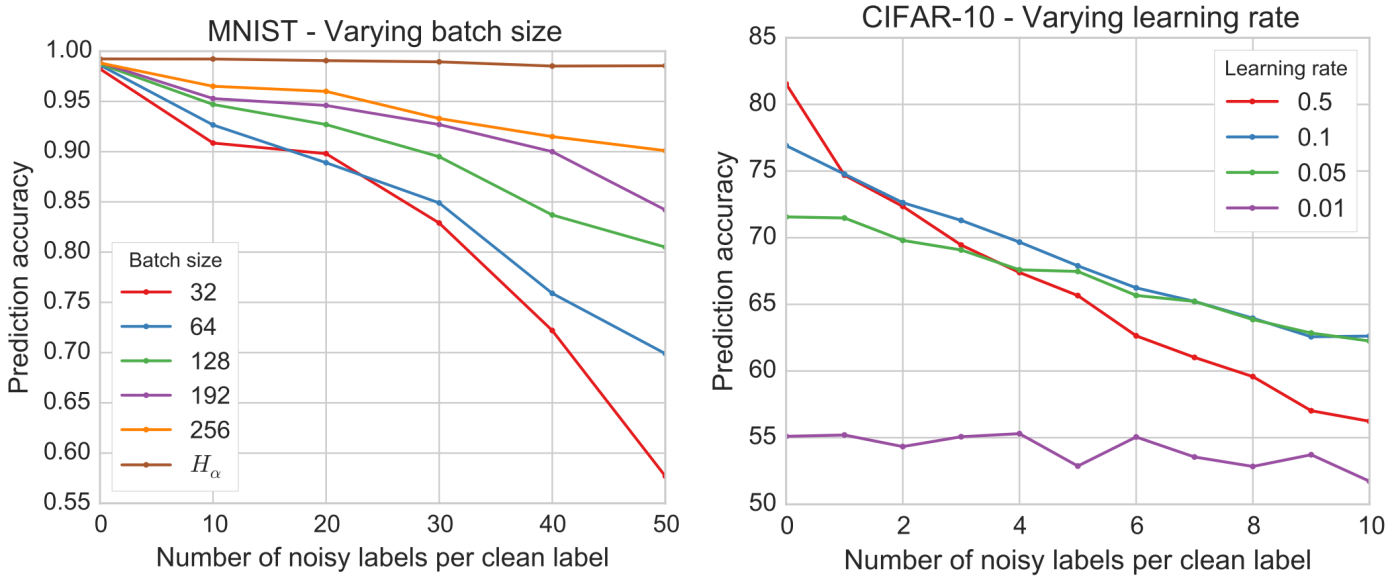
- 배치 사이즈가 커질수록 noisy data에 강건해지는 경향이 있습니다.
- 학습률이 작아질수록 noisy data에 강건해지는 경향이 있습니다.
먼저 아래의 왼쪽 figure를 보시면 배치 사이즈에 대해 주장하는 바가 명확합니다. clean label 당 noisy label의 개수가 50일때를 보면 배치 사이즈가 커질 수록 noisy label에 더욱 강건한 모델이 구축됨을 알 수 있습니다. 참고로 \(H_\alpha\)는 배치 사이즈를 무한대로 보았을 때의 결과입니다. 실제 실험을 할 때는 배치 사이즈를 무한대로 하는 것은 불가능한데요. 저자는 손실 함수 부분을 수정하여 이론적으로 배차 사이즈가 무한일 때를 환경을 구축하여 실험을 하였습니다. 해당 부분에 대해서 자세히 알고 싶으신 분들은 논문을 참고해 주시길 바랍니다. 저자는 미니 배치 학습시 배치 단위의 loss는 평균을 내어 도출되는데요, 저자는 이와 같은 로직에 의해서 noisy label에 대한 잘못된 loss는 cancel out 되며, correct label의 gradient에 대한 기여도가 더 많이 반영된다고 해석합니다. 다시말해, ‘평균’이라는 로직에 때문에, 배치 사이즈가 증가할 수록 평균 gradient는 correct label의 gradient에 점점 가까워 짐을 뜻합니다.
아래의 오른쪽 figure는 학습률과 정확도의 관계를 보여줍니다. 일반적으로 뉴럴넷 학습시 배치 사이즈를 증가시키면 학습률도 같이 scale up 하게 됩니다. 특히 배치사이즈가 작아질수록 optimal 학습률도 역시 작아지는 경향이 있다는 연구 결과도 있습니다 [3]. 저자는 실험을 통해서 noisy label의 개수의 증가는 effective 배치 사이즈를 감소시키는 결과를 초래함을 관찰하였습니다. 따라서 noisy data가 증가하면 effective 배치 사이즈가 작아지므로 optimal 학습률도 작아져야 하므로 이러한 결과한 발생하였다고 주장합니다. 개인적으로 근거가 부족하지 않나라는 생각을 해봅니다. 특히 아래의 오른쪽 figure를 보면 가장 작은 학습률 값은 0.01인데, 0.01의 prediction accuracy가 가장 낮습니다. 따라서 데이터셋을 달리하거나 실험 환경을 조금만 수정해도 아예 다른 결과가 도출되지 않을까라는 생각이 듭니다.
4 덧 붙이는 말
실무에서 다루는 데이터는 대부분 noisy가 포함되게 됩니다. 특히 최근에 업무를 수행하면서 noisy data 처리 문제에 대해 많은 고민을 하게 되었는데요, 역시 가장 확실한 방법은 noisy data를 clean data로 만드는 것입니다. 가장 강력하지만 가장 많은 비용을 수반하죠. 다시말해 현실적으로 불가능한 경우가 많다라는 것입니다. 그렇다면 noisy data를 어느 정도 감안하고 학습해도 될까요? 본 논문에 이에 대한 답을 간접적으로 나마 제안합니다. noisy data의 특성과 크기에 따라, 또 달성하고자 하는 accuracy에 따라 clean label을 생성하는데 수반되는 성능과 비용을 trade-off 관계를 잘 고려하여 의사결정을 해라는 것이 이 논문에서 핵심적으로 주장하려는 바인 것 같습니다. 그러나 해당 논문의 결과는 데이터셋에 따라 크게 달라질 수 있기 때문에 참고용 정도로만 활용해야할 것 같습니다.
Reference
[2] Deep Learning is Robust to Massive Label Noise - Paper Review
