T-SNE는 고차원의 임베딩을 저차원으로 변환하고 시각화화여 임베딩을 품질들 대략적으로 파악하는 것을 돕는 대표적인 차원 축소 알고리즘입니다. 실제로 아직도 현업에서도 많이 사용되는 알고리즘이고, 여러 논문에서도 임베딩의 질을 시각적으로 보여주기 위한 방법으로 많이 활용되고 있습니다.
그러나 어느 순간 T-SNE의 원리를 완벽하게 이해하지 못하고 사용하고 있다는 생각이 들었습니다. 🫠 앞으로 현업에서 임베딩을 다룰 일이 많아질 것 같은 느낌이 들어서 이번 기회에 정확한 동작 원리를 공부해보았습니다. 공부해보니 ML 기초 이론을 복습하기에도 좋은 알고리즘이라는 생각이 들더라구요. 앞으로 설명 드릴 내용은 다음의 배경 지식을 요구합니다.
- Gaussian distribution
- Student-T distribution
- KL-Divergence
- Gradient decent
Summary
- T-SNE는 고차원 데이터를 저차원으로 내릴 때, 주변 이웃 정보를 최대한 보존하는 알고리즘입니다.
- 고차원에서 가까운 데이터는 저차원에서도 가깝게 만드는 것이 목표입니다. 이를 위해 기초 통계, 최적화 이론을 활용합니다.
T-SNE = Gaussian + Student T + KL-Divergence + Gradient Decent
T-SNE의 핵심 작동 원리는 4개의 키워드로 표현할 수 있습니다.
- Gaussian distribution: 고차원 공간(원래 벡터들이 존재하는 공간)을 가우시안 분포로 표현합니다. 이때 원래 가까운 벡터들은 높은 확률값을 갖도록, 그 반대는 반대가 되도록 합니다.
- Student T-distribution: 저차원 공간(시각화를 위한 공간, 일반적을 2~3차원)을 T 분포로 표현합니다. 이때 고차원에서 원래 가까운 벡터들은 높은 확률을 가지도록, 그 반대는 반대가 되도록 표현하는 T 분포를 찾는 것이 목표입니다.
- KL-Divergence: 가우시안 분포와 T 분포가 차이가 나는 정도를 계산합니다.
- Gradient Decent: KL-Divergence의 값에 대한 저차원 벡터의 gradient를 계산하고, KL-Divergence가 작아지는 방향으로 저차원 벡터를 점진적으로 이동시킵니다.
예시로 학습 방식 직관적으로 이해해 보기
T-SNE의 학습 방식을 예시를 들어봅시다. 직관적으로 이해하기 쉬울 거예요. T-SNE는 먼저 고차원에서 각 데이터 포인트(예: 학생 A, B)가 서로 얼마나 가까운지를 계산합니다.
- 가까우면: 이 둘은 서로 비슷하네
- 멀면: 이 둘은 서로 다르네
같은 말을 확률로 표현하면 이렇게도 표현할 수 있습니다.
- 가까우면: 이 둘이 서로 친구일 확률은 0.8
- 멀면: 이 둘이 서로 친구일 확률은 0.1
이제 데이터 포인트를 저차원 공간(예: 2차원)에 배치하는데, 이 때 위에서 계산한 친구일 확률을 최대한 유지하는 것이 중요합니다.
- 고차원에서 가까웠다면: 저차원 공간에서도 서로 친구일 확률을 크게
- 고차원에서 멀었다면: 저차원 공간에서도 서로 친구일 확률을 작게
고차원 공간의 확률과 저차원 공간의 확률 구조를 비슷하게 유지하기 위해서 벌점을 부과합니다.
- 고차원에서 가까웠지만(확률 큼) 저차원에서 멀면(확률 작음): 벌점이 커짐
- 고차원에서 가까웠고(확률 큼) 저차원에서도 가까우면(확률 큼): 벌점이 작아짐
마지막으로 이 벌점을 줄이기 위한 방향으로 저차원 공간의 데이터 포인터를 점진적으로 이동시킵니다.
- 벌점이 큰 벡터: 벌점이 작아지는 방향으로 크게 이동 시킴
- 벌점이 작은 벡터: 벌점이 작아지는 방향으로 작게 이동 시킴
수식과 함께 더 자세히 이해해 보기
T-SNE의 학습 방식을 예시를 통해 직관적으로 이해해 보았습니다. 이제 수식을 곁들여서 좀 더 자세히 이해해 보죠!
고차원 확률 분포 정의 - 가우시안 분포
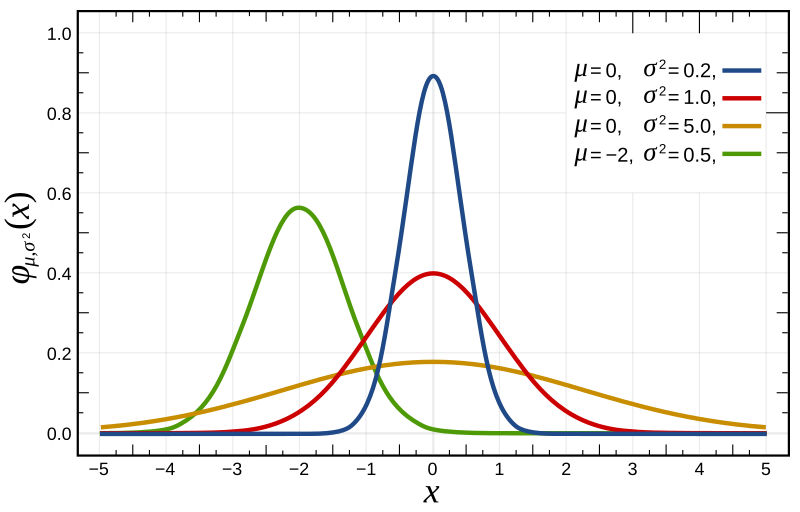가우시안 분포
T-SNE는 고차원 공간에 데이터 포인트 \(x_i, \cdots, x_N\)가 있을 때(\(i \neq j\)) \(x_i\)와 \(x_j\)의 유사도(거리)에 비례하는 확률 분포 \(p_{ij}\)를 계산하는 것이 첫번째 목표입니다. 이를 위해 \(x_i\)가 \(x_j\)를 이웃으로 선택할 확률 \(p_{j \mid i}\)를 조건부 확률로 나타냅니다. 이 때, \(p_{i \mid i} = 0\)이고 \(\sum_{j}P_{j \mid i}=1, \forall i\)입니다.
\[p_{j \mid i} = \frac{\exp\!\left(-\| \mathbf{x}_i - \mathbf{x}_j \|^2 / 2\sigma_i^2 \right)} {\sum_{k \neq i} \exp\!\left(-\| \mathbf{x}_i - \mathbf{x}_k \|^2 / 2\sigma_i^2 \right)}\]이 수식은 \(\mathbf{x}_i\)를 평균으로 하는 가우시안 분포의 수식과 사실상 같다는 것을 알 수 있습니다.
\[N(x; \mu, \sigma^2) = \cfrac{1}{\sqrt{2\pi\sigma^2}} \exp(- (x-\mu)^2/2\sigma^2)\]즉, 고차원 공간에서의 벡터의 거리를 확률로 변환하는데 이때 가우시안 분포를 활용한다는 것을 알 수 있습니다. 또한 \(p_{j \mid i}\)의 분모의 수식에 의해 식이 노말라이즈 되면서 \(\sum_{j}P_{j \mid i}=1, \forall i\)가 만족될 수 있음을 알 수 있습니다.
마지막으로 조건부 확률을 대칭 확률로 변환하여 이는 \(x_i\)와 \(x_j\)가 이웃일 최종 확률을 구합니다. 이렇게 하는 이유는 \(p_{j \mid i}\)와 \(p_{i \mid j}\)의 분포가 다르기 때문입니다(분모가 다릅니다).
\[p_{ij} = \cfrac{p_{j \mid i} + p_{i \mid j}}{2N} \text{, where N=number of dimension}\]아직 \(p_{j \mid i}\)을 계산하기 위해 필요한 \(\sigma_i^2\)를 설명하지 않았습니다. 이 값은 \(x_i\)를 중심으로 한 가우시안 분포의 분산입니다. 하지만 이 값은 아직 정확히 계산할 수는 없습니다. 이렇게 생각할 수도 있습니다.
“그냥 기초적인 분산 공식에 따라 계산할 수 있는 거 아니야?”
사실은 맞는 말입니다. 그러나 T-SNE 알고리즘은 이렇게 하진 않고, 실질적으로 몇 개의 이웃 데이터 포인트만 중요하게 생각할지에 따라서 분산을 결정하는 전략을 취하고 있습니다. 그리고 이 분산을 정하기 위해서 perplexity라는 하이퍼파라미터를 도입합니다. 직관적으로 생각 해보면, 더 많은 데이터 포인트를 실질적인 이웃이라고 고려할수록 분산은 커지고, 그 반대는 반대가 될 겁니다. 여기서는 이 하이퍼파라미터가 왜 필요한지만 직관적으로 이해하고 넘어가고, perplexity는 아래에서 더 자세히 설명하겠습니다.
저차원 확률 분포 정의 - T 분포
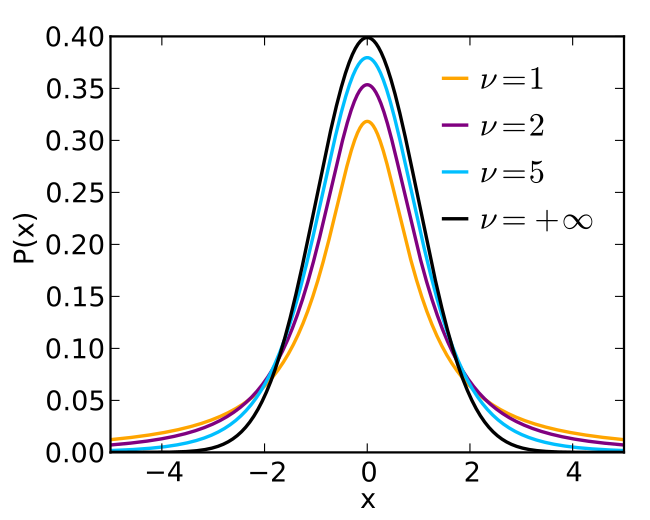자유도에 따른 Student-t 분포
저차원에서는 T 분포에 기반하여 두 벡터간의 거리를 확률의 개념으로 표현하는 것만 제외하면 위 접근법과 거의 유사합니다. 저차원 공간에 \(y_1, \cdots, y_N (y_i \in \mathbb{R}^d)\) 데이터 포인트가 존재할 때, 아래 수식으로 두 데이터 포인트 \(y_i\)와 \(y_j\) 사이의 거리(유사도)를 확률 \(q_{ij}\)로 변환합니다.
\[q_{ij} = \frac{(1 + \| \mathbf{y}_i - \mathbf{y}_j \|^2)^{-1}} {\sum_k \sum_{l \neq k} (1 + \| \mathbf{y}_k - \mathbf{y}_l \|^2)^{-1}}\]이 수식은 자유도가 1인 student t-분포와 사실상 같다는 것을 알 수 있습니다. 먼저 student t-분포의 PDF는 다음과 같습니다.
\[f(t; \nu) = \frac{\Gamma\!\left(\tfrac{\nu+1}{2}\right)}{\sqrt{\pi \nu}\,\Gamma\!\left(\tfrac{\nu}{2}\right)}\left(1 + \frac{t^2}{\nu}\right)^{-\tfrac{\nu+1}{2}}\]이때 \(\nu = 1\)이라고 한다면, 다음과 같이 표현할 수 있습니다.
\[f(t) = c\left(1 + t^2\right)^{-1}\]저차원 데이터 포인트 업데이트 - KL-Divergence & gradient descent
지금까지 논의를 통해서 원래 고차원 공간에서의 데이터 포인트 간의 거리를 확률로 표현하고, 비슷한 방법으로 저차원 공간에서의 데이터 포인트 간의 거리를 확률로 표현하는 방법을 살펴 보았습니다. 그렇다면, 저차원 공간에서 결정된 데이터 포인트가 잘 사상된 것인지 어떻게 검증할 수 있을까요? 그리고 데이터 포인트를 더 적절한 위치로 옮기려면 어떻게 해야할까요? 이때 딥러닝의 학습의 기반이 되는 유명한 KL-Divergence와 gradient descent가 활용됩니다.
먼저, KL-Divergence는 아래의 수식이고, 이 수식은 확률 분포 \(p_{ij}\)와 \(q_{ij}\)의 차이를 측정하게 됩니다.
\[KL(P \parallel Q) = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}\]마지막으로 계산된 KL-Divergence를 \(y_{i}\)에 대해 미분하여 gradient를 얻고, 이를 활용하여 \(y_i\)의 값을 변경하는 gradienct descent를 적용하게 됩니다. 결과적으로 따라서 T-SNE는 고차원 공간에서의 분포를 잘 반영할 수 있는 저차원 공간을 찾는 차원 축소 알고리즘이라고 볼 수 있습니다.
\[y_i \leftarrow y_i - \eta \cfrac{\partial KL(P \parallel Q)}{\partial y_i}{}\]Perplexity
perplexity란 \(x_i\)가 실질적으로 혹은 중요하게 고려하는 이웃 데이터 포인트, 즉 유효 이웃 수를 의미합니다. 이 값이 중요한 이유는 이에 따라 \(\sigma_i^2\)가 결정되기 때문입니다.
- perplexity가 클수록 분산 \(\sigma_i^2\)도 커집니다.
- perplexity가 작을수록 분산 \(\sigma_i^2\)도 작아집니다.
위에서 이론적으로는 분산 공식에 따라 \(\sigma_i^2\)를 구할 수는 있지만, T-SNE는 그렇게 하지 않는다고 언급 했습니다. T-SNE는 굳이 perplexity라는 하이퍼파라미터를 통해 적절한 분산 \(\sigma_i^2\)을 구합니다. 도대체 이유가 뭘까요? 그 이유는 데이터의 지역 밀도(local density)를 고려해서, 모든 데이터 포인트가 유사한 유효 이웃 수를 갖도록 균형을 맞추기 위함입니다.
아래 그래프는 perplexity=5일 때, 밀집 영역에 있는 빨강 데이터 포인트와 희소 영역에 있는 파랑 데이터 포인트에 대해서 분산 공식에 따라 전역 분산을 구했을 때의 가우시안 분포(점선)와 perplexity에 따라 국소 분산을 구했을 때의 가우시안 분포(실선)을 시각화 했습니다.
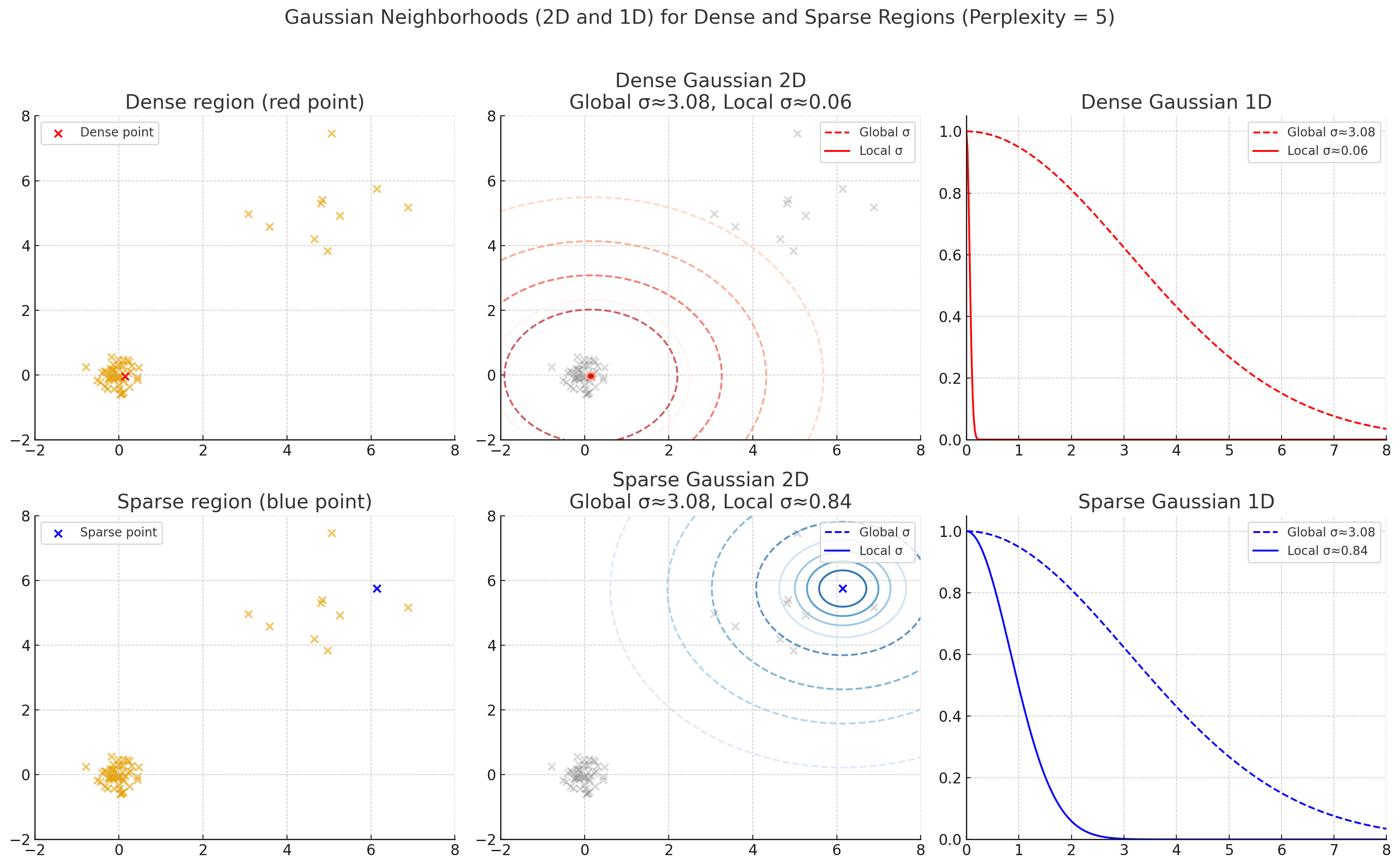perplexity=5일 때, 지역 밀집도에 따른 가우시안 분포
- 국소 분산(실선): 데이터의 밀집도를 반영하여 본인 주위의 일부만을 유효 이웃으로 고려하고 있습니다.
- 전역 분산(점선):데이터의 밀집도를 반영하지 못하고, 클러스터 내의 모든 데이터 포인트를 유효 이웃으로 고려하고 있습니다.
정리하면, T-SNE는 데이터의 지역 구조를 보존하기 위해 일반적인 분산 공식에 의한 전역 분산을 사용하지 않고, perplexity라는 값에 기반한 국소 분산을 활용한다고 할 수 있습니다. 일반적으로 perplexity는 5~50 사이의 값으로 설정한다고 합니다.
perplexity는 shannon entropy에 기반한 다음의 공식을 따릅니다.
\[\text{Perplexity}(P_i) = 2^{-\sum p_{j \mid i} \log_2{p_{j \mid i}}}\] \[\text{where} -\sum p_{j \mid i} \log_2{p_{j \mid i}} \text{ is Shannon entropy}\]만약 \(\text{Perplexity}(P_i)=5\)라고 설정 했으면, \(2^{-\sum p_{j \mid i} \log_2{p_{j \mid i}}}=5\)를 만족하는 분산 \(\sigma_i^2\)을 찾으면 됩니다.
T-SNE의 단점과 변형 알고리즘들
T-SNE의 최대 단점은 데이터 포인트가 \(N\)개 일때, 한 이터레이션에서 \(N^2\)개의 쌍을 비교하는 연산이 필요하다는 것입니다. 즉, 시간 복잡도가 \(O(N^2)\)입니다. 이를 극복하기 위해 다양한 변형 알고리즘들이 있으니 참고해보세요.
- Barnes-Hut t-SNE: \(O(N \log N)\)
- Flt-SNE: \(O(N)\)
Laurens van der Maaten(T-SNE 저자)의 FAQ
How should I set the perplexity in t-SNE?
- The performance of t-SNE is fairly robust under different settings of the perplexity.
- The most appropriate value depends on the density of your data. Loosely speaking, one could say that a larger / denser dataset requires a larger perplexity.
- Typical values for the perplexity range between 5 and 50.
What is perplexity anyway?
- In t-SNE, the perplexity may be viewed as a knob that sets the number of effective nearest neighbors.
- It is comparable with the number of nearest neighbors k that is employed in many manifold learners.
Every time I run t-SNE, I get a (slightly) different result?
- In contrast to, e.g., PCA, t-SNE has a non-convex objective function.
- The objective function is minimized using a gradient descent optimization that is initiated randomly. As a result, it is possible that different runs give you different solutions.
- Notice that it is perfectly fine to run t-SNE a number of times (with the same data and parameters), and to select the visualization with the lowest value of the objective function as your final visualization.
참고자료
- t-distributed stochastic neighbor embedding
- Student’s t-distribution
- https://lvdmaaten.github.io/tsne/