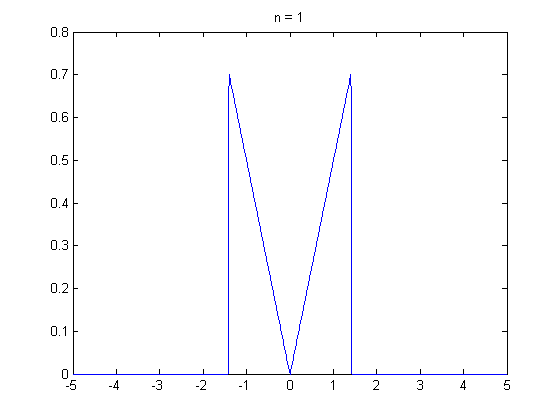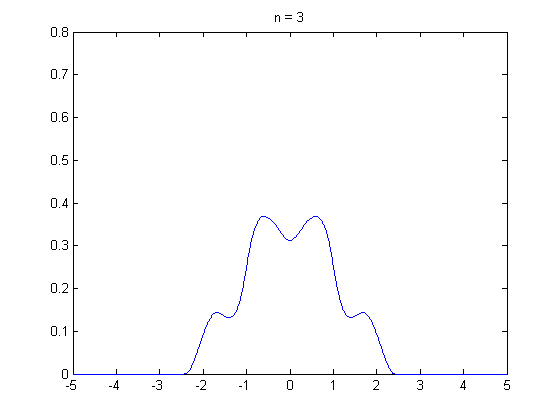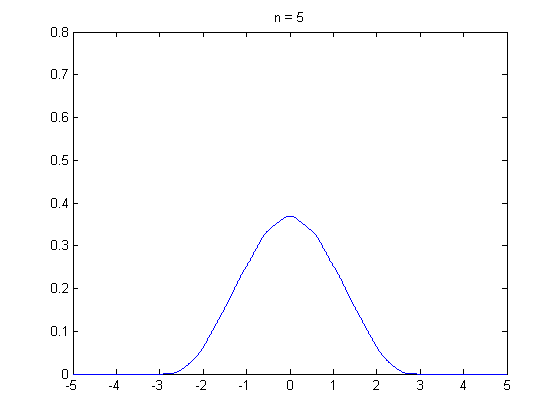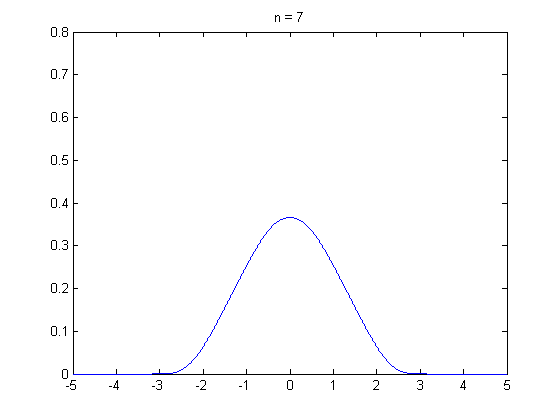
석사과정 때부터 중심극한정리에 의해서 표본의 크기가 30 이상이면 정규분포가 되어서…’ 라는 말을 많이 들어왔습니다. 그래서 ‘설문자료를 수집할 때 표본이 30개 이상이면 분석을 할 수 있겠구나…’ 라고 단순하게 생각 했던 때가 있었는데요. 최근에 하버드 확률론 기초 강의(Statistics 110)를 수강하면서 수업 말미에 등장한 중심극한정리에 대한 내용을 들으면서 제가 너무 단순하게 알고 있었다는 것을 깨달았습니다. 그래서 이 주제로 정리를 꼭 한번 해봐야지라고 생각하고 있었는데, 제가 생각 했던 것 보다 어려운 개념이었습니다… 😩 이 분야를 공부하면 정말 겸손해지네요. 아무튼 제가 아는 선에서 중심극한정리에 대한 내용을 담아 냈습니다. 틀린 부분 있으면 지적해 주시면 감사하겠습니다.
1 중심 극한 정리(Central Limit Theorem, CLT)란?
정의
중심 극한 정리란 i.i.d. 확률 변수 \(X_1, X_2, ...\) 가 표본의 크기 \(n\)이 \(\infty\)에 다가가면, 표본평균 \(\bar{X}\)의 분포가 정규 분포에 분포 수렴한다는 정리을 말합니다. 만약 표본 평균이 표준화(standardization)된 상태(\(\mu=0, \sigma^2=1\))이면 표준 정규 분포에 수렴합니다.
큰수의 법칙으로는 표본의 분포(shape)를 알 수 없다.
먼저 큰수의 법칙을 다시 상기해 봅시다. 큰수의 법칙은 모집단에서 추출한 표본 \(X_1, X_2, \cdots, X_n\) 이 i.i.d. 이면서 평균 \(\mu\), 분산 \(\sigma^2\)를 따를 때, \(n \rightarrow \infty\)이면 \(\bar{X}\)가 1의 확률로 \(\mu\)에 수렴함을 말합니다. 그러나 큰수의 법칙은 표본 평균 \(\bar{X}\)의 shape 즉, 분포 대해서는 전혀 알려 주지 못합니다.
중심 극한 정리는 표본의 분포(shape)를 설명할 수 있다.
그렇다면 \(n \rightarrow \infty\)일때, \(\bar{X}\)의 분포는 어떤지 알 수 있을까요? 결론적으로 말하면 중심 극한 정리를 통해 표본 평균 \(\bar{X}\)의 분포를 설명할 수 있습니다. 중심 극한 정리는 모집단에서 크기가 \(n\)인 표본 \(X_1, X_2, \cdots, X_n\)을 임의 복원 추출 했을 때 \(n \rightarrow \infty\) 이면 표본평균 \(\bar{X}\)는 정규 분포에 수렴한다는 것을 말합니다. 만일 표본 평균 \(\bar{X}\)가 표준화(standardization)되었다면, 표준 정규 분포에 수렴합니다.
\[\text{As } n \rightarrow \infty, \\\] \[\cfrac{\sqrt{n}\big(\bar{X}_{n}-\mu \big)}{\sigma} \rightarrow N(0,1)\]참고로 표준화 되지 않은 표본 평균은 \(n\)이 충분히 크다면, 평균 \(\mu\), 분산 \(\cfrac {\sigma^2} {n}\)인 정규분포를 따릅니다.
\[\text{As } n \rightarrow \infty,\\[1em]\] \[\bar{X}_n \rightarrow N\bigg(\mu, \cfrac{\sigma^2}{n}\bigg)\]2 표본 평균의 평균과 분산 계산
표본 평균은 확률 변수
먼저 반드시 헷갈리지 말아야 할 것이 표본 평균(sample mean)은 확률 변수라는 점입니다. 따라서 표본 평균은 기대값(표본평균의 평균), 분산(표본평균의 분산), 표준 편차(표본평균의 표준편차)를 가지게 됩니다. 말이 굉장히 헷갈릴 수 있으므로 주의해서 살펴보셔야 합니다.
표본 평균의 평균(기대값)
\[\begin{aligned} E(\bar{X}_n) &= E\bigg(\cfrac{1}{n}\bigg(X_1+\cdots+X_n\bigg)\bigg) \\ &= \cfrac{1}{n}E\bigg(X_1+\cdots + X_n \bigg) \\ &= \cfrac{1}{n}\bigg(E(X_1)+\cdots+E(X_n)\bigg) \\ &= \cfrac{1}{n} \cdot n \cdot \mu \\ &= \mu \end{aligned}\]표본 평균의 표준편차
\[\begin{aligned} Var(\bar{X}_n) &= Var\bigg(\cfrac{1}{n}\bigg(X_1+\cdots+X_n\bigg)\bigg) \\ &= \cfrac{1}{n^2}\cdot Var\bigg(X_1+ \cdots + X_n \bigg) \\ &= \cfrac{1}{n^2} \cdot \bigg(Var(X_1)+\cdots+Var(X_n)\bigg) \\ &= \cfrac{1}{n^2} \cdot n \cdot \sigma^2 \\ &= \cfrac{\sigma^2}{n} \\ \therefore \space SD(\bar{X}_n) &= \cfrac{\sigma}{\sqrt{n}} \end{aligned}\]표본 평균의 표준화
먼저 표준화는 다음의 수식을 따릅니다. 그 결과 평균이 0, 분산 1이 되는 분포로 변화됩니다.
\[\cfrac{X-E(X)}{\sigma}\]이를 활용해 표본 평균을 표준화 하면 아래의 값이 도출 됩니다.
\[\begin{aligned} \cfrac{\bar{X}_n-E(\bar{X}_n)}{SD(\bar{X}_n)} &= \cfrac{\bar{X}_n-\mu}{\cfrac{\sigma}{\sqrt{n}}} \\[1em] &= \cfrac{\sqrt{n}(\bar{X}_n-\mu)}{\sigma} \end{aligned}\]참고로 표준화의 의미는 평균을 0, 분산을 1로 강제하는 것이지만 단순히 scaling, shift를 한 것이지 원래의 분포의 모양 자체를 바꿀 수는 없습니다. 다시 말해 표준화 한다고 해서 원래 정규 분포가 아닌 어떤 분포가 표준 정규 분포로 바뀌는 것은 아닙니다. 아래 그림을 보면 원래 분포(Before)를 표준화하여 \(\mu=0, \sigma^2=1\)로 만들었는데요. 그 결과가 표준 정규 분포가 아닙니다.

3 중심 극한 정리는 왜 중요할까?
위에서 중심 극한 정리가 어떤 의미인지 살펴보았습니다. 그런데 중심 극한 정리의 놀라운 점은 i.i.d. 가정이 충족되고 유한한 평균 \(\mu\) 및 분산 \(\sigma^2\)만 정의 된다면 원래의 분포 \(X_j\)의 어떠한 정보가 없더라도 표본 평균의 분포가 표평균 \(\mu\), 분산 \(\cfrac{\sigma^2}{\sqrt{n}}\)인 정규 분포에 가까워 진다는 것을 알려 준다는 점입니다.
따라서 우리는 중심 극한 정리에 기반하여, 표본의 크기가 충분하다면 내가 수집한 표본의 표본 평균이 발생할 확률을 정규 분포에서 계산할 수 있게 됩니다. 특히 이러한 통계적 추론은 모집단의 분포가 어떤 모양이든지 관계 없이 가능 하다는 점에서 엄청난 편의성을 제공합니다. 정리하자면, 중심 극한 정리는 표본 평균과 모집단 간의 관계를 나타냄으로써 표본 통계량(statistics)를 이용해 모수(parameter)를 추정할 수 있는 수학적 근거를 제시합니다. 따라서 중심 극한 정리는 통계에서 가장 중요한 이론적 근거라고 하겠습니다.
여기부터는 사견입니다. 왜 모집단의 ‘분포’ 자체를 추정하지 않고 모집단의 ‘모수’를 추정하려고 할까요? 그 이유는 2가지 인 것 같습니다. 먼저, 모집단의 분포를 우리는 알 수 없습니다. 모집단의 분포를 알 수 없기에 통계적 추정을 하는 것이죠. 그리고 어떤 분포의 모수(모평균, 모분산 등)를 알면 그 분포를 거의 정확하게 그려 낼 수 있습니다. 우리가 흔히 들어 본 정규 분포, 이항 분포, 베타 분포 등 다양한 분포는 평균과 분산만 알면 그 PDF, PMF 식을 알 수 있습니다.
4 중심 극한 정리를 증명해 보자!
적률 생성 함수의 성질
증명을 위해서는 MGF(적률 생성 함수), 로피탈의 정리에 대한 사전 지식이 필요합니다. 이와 관련해서는 쉽고 자세 하게 정리된 글들이 많으니 자세한 내용은 해당 글들을 먼저 참고 부탁드립니다 🙏 간단히 언급하자면, 다음과 같은 적률 생성 함수의 성질에 대한 사전 지식이 필요합니다.
- 확률 변수 \(X\), \(Y\)가 독립이라면, \(M_{X+Y}(t) = M_{X}(t)M_{Y}(t)\)
- 어떤 두 확률 분포의 적률 생성 함수가 동일하면, 두 확률 분포는 동일합니다.
증명 순서
이제 수식을 통해 증명을 해보겠습니다. 증명 순서는 다음과 같습니다.
- 표준화(standardization)한 표본 평균의 적률 생성 함수를 구합니다.
- 해당 함수를 \(n \rightarrow \infty\)로 보내 봅니다.
- 이 때 구해지는 적률 생성 함수가 표준 정규 분포의 적률 생성 함수와 동일하다는 것을 확인합니다.
- 따라서 표본의 크기가 충분히 클때 표본 평균은 표준 정규 분포에 분포 수렴한다는 결론을 내립니다. 먼저 표준화한 표본 평균의 적률 생성 함수를 구해보겠습니다.
증명 과정
\[\begin{align} M_{\tfrac{\sqrt{n}(\bar{X}-\mu)}{\sigma}}(t) &= M_{\tfrac{\sqrt{n}(\tfrac{1}{n}(X_1+\cdots+X_n)-\mu)}{\sigma}}(t) \\[1em] &= M_{\tfrac{(X_1 + \cdots + X_n)-n\mu }{\sigma \sqrt{n}}}(t) \\[1em] &= M_{\tfrac{X_1-\mu}{\sigma} + \cdots + \tfrac{X_n-\mu}{\sigma}}(t) \\[1em] &= M_{\tfrac{X_1-\mu}{\sigma}}(t) M_{\tfrac{X_2-\mu}{\sigma}}(t) \cdots M_{\tfrac{X_n-\mu}{\sigma}}(t) \\[1em] &= E\Big(\text{exp}\Big(\tfrac{(X_1-\mu)t}{\sigma\sqrt{n}}\Big)\Big) E\Big(\text{exp}\Big(\tfrac{(X_2-\mu)t}{\sigma\sqrt{n}}\Big)\Big) \cdots E\Big(\text{exp}\Big(\tfrac{(X_n-\mu)t}{\sigma\sqrt{n}}\Big)\Big) \\[1em] &= \Big\{ E\Big(\text{exp}\Big(\tfrac{(X-\mu)t}{\sigma\sqrt{n}}\Big)\Big) \Big\}^n \\[1em] &= \Big\{ M_{\tfrac{X-\mu}{\sigma}} \Big( \tfrac{t}{\sqrt{n}} \Big) \Big\}^n \\[1em] \end{align}\]여기까지 표준화한 표본 평균의 적률 생성 함수를 유도했습니다. 이제 해당 함수를 \(n \rightarrow \infty\)으로 보내려고 하는데요. 약간의 문제가 있습니다. 위에서 유도한 식에 극한을 취해서 \(n \rightarrow \infty\)로 보내면 \(1^{\infty}\)라는 값이 등장하게 됩니다. 그래서 자연로그를 취한 후 극한을 취하는 테크닉을 적용하게 됩니다.
\[\begin{align} \lim_{n \rightarrow \infty} \text{ln} \Big\{ M_{\tfrac{X-\mu}{\sigma}} \Big( \tfrac{t}{\sqrt{n}} \Big) \Big\}^n &= \lim_{n \rightarrow \infty} n \text{ln} M_{\tfrac{X-\mu}{\sigma}} \Big( \tfrac{t}{\sqrt{n}} \Big) \\[1em] &= \lim_{y \rightarrow 0} \frac{\text{ln} M_{\tfrac{X-\mu}{\sigma}}(yt)}{y^2} \space\space\space\space\space\space\space\space\space\space\space\space\space \text{where } y=\frac{1}{\sqrt{n}} \\[1em] &= \lim_{y \rightarrow 0} \frac{\cfrac{tM'(yt)}{M_{\tfrac{X-\mu}{\sigma}}(yt)}}{2y} \space\space\space\space\space\space\space\space\space\space\space\space\space\space \text{by L’Hˆopital’s rule} \\[1em] &= \lim_{y \rightarrow 0} \frac{tM'_{\tfrac{X-\mu}{\sigma}}(yt)}{2y} \\[1em] &= \cfrac{t}{2} \lim_{y \rightarrow 0} \frac{M'_{\tfrac{X-\mu}{\sigma}}(yt)}{y} \\[1em] &= \cfrac{t}{2} \lim_{y \rightarrow 0} \cfrac{tM''_{\tfrac{X-\mu}{\sigma}}(yt)}{1} \\[1em] &= \cfrac{t^2}{2} \lim_{y \rightarrow 0} M''_{\tfrac{X-\mu}{\sigma}}(yt) \space\space\space\space\space\space\space\space\space\space\space\space\space\space \text{by L’Hˆopital’s rule} \\[1em] &= \cfrac{t^2}{2} M''(0) \\[1em] &= \cfrac{t^2}{2} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space \text{by MGF of standard normal dist.} \end{align}\]위 식이 말하고자 하는 것은 \(n \rightarrow \infty\) 일 때,
\[\text{ln} \bigg\{ M_{\tfrac{X-\mu}{\sigma}}\bigg(\frac{t}{\sqrt{n}}\bigg) \bigg\}^n \rightarrow \frac{t^2}{2}\]화살표 왼쪽은 증명의 첫 출발점이었던 표준화한 표본 평균의 MGF에 자연로그를 취한 것과 동일합니다. 따라서
\[\text{ln }M_{\tfrac{\sqrt{n}(\bar{X}-\mu)}{\sigma}}(t) \rightarrow \frac{t^2}{2}\]최종적으로 \(n \rightarrow \infty\) 일 때 표준화된 표본 평균의 MGF는 표준 정규 분포의 MGF \(\big(=e^{t^2/2}\big)\)와 같으므로 표준화된 표본 평균은 표준 정규 분포에 분포 수렴한다는 사실을 증명할 수 있습니다.
\[M_{\tfrac{\sqrt{n}(\bar{X}-\mu)}{\sigma}}(t) \rightarrow e^{t^2/2}\]참고자료
- 중심극한정리 - 위키피디아
- 중심극한 정리는 무엇이고 왜 중요한가?
- Can any data be transformed into a standard normal distribution?
- “Introduction to Probability”, Joseph K. Blitzstein, Jessica Hwang
