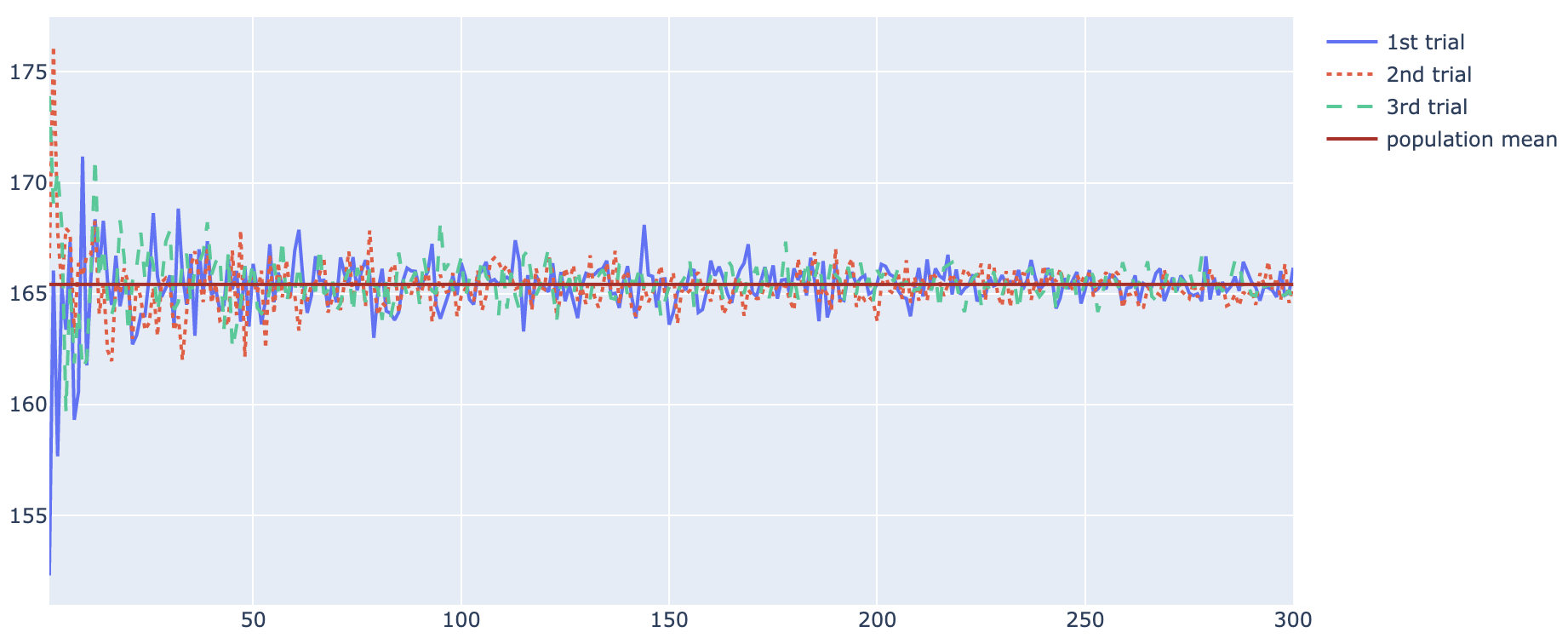
표본의 크기가 커질수록 표본평균은 모평균에 근접해 갑니다.
우리는 공정한 동전을 던졌을 때 앞면이 나타날 확률이 \(\cfrac{1}{2}\)이라는 것을 특별히 증명하지 않아도 알 수 있습니다. 우리가 지금까지 살아오면서 겪은 수많은 경험들에 의하면 동전의 앞면이 나타날 확률이 \(\cfrac{1}{2}\)이기 때문이죠. 이처럼 수많은 경험의 경향성, 다시 말해 수많은 표본에 따른 평균(표본평균)이 실제 평균(모평균)에 다가가는 현상을 큰수의 법칙이라고 일컫습니다. 한편 큰수의 법칙과 가장 헷갈릴만한 개념이 중심 극한 정리(CLT)일 것입니다. 이 글의 끝에는 중심 극한 정리와의 차이점을 간략하게 짚고 넘어 가겠습니다. 중심 극한 정리에 대해 더욱 자세하게 알고 싶으신 분들은 여기를 참고 해주세요.
1 큰수의 법칙(LLN, Law of Large Numbers)
정의
먼저 평균이 \(\mu\), 분산이 \(\sigma^2\)인 i.i.d. 확률 변수 \(X_1, X_2, ...\) 가 있다고 가정해 봅시다. 이 때 \(X_1\)에서 \(X_n\)까지의 평균을 표본 평균 \(\bar{X}_n\)이라고 하고 다음과 같이 계산할 수 있습니다.
\[\bar{X}_n = \cfrac{X_1 + \cdots + X_n}{n}\]큰수의 법칙이란 표본의 크기 \(n\)이 증가함에 따라 표본 평균 \(\bar{X}_n\)이 모평균 \(\mu\)에 수렴하는 현상을 말합니다. 큰수의 법칙은 시뮬레이션, 통계학, 과학 등에서 필수적인 개념입니다. 시뮬레이션 상황 또는 현실 세계에서 독립적인 표본을 추출(생성, generating)하는 실험을 반복한다고 생각해 봅시다. 우리는 이론적인 평균값(theoretical average)을 추정하기 위해서 자연스럽게 표본들에서 알 수 있는 평균값(average value in the replications)을 활용하고자 할 것입니다. 이 같은 사실은 우리는 우리도 모르는 사이에 큰수의 법칙을 활용하고 있는 셈이죠!! 큰수의 법칙은 큰수의 강법칙(SLLN)과 큰수의 약법칙(WLLN), 두 가지 버전으로 나눌 수 있습니다. 두 가지 버전은 개념적으로 약간의 차이가 존재하지만, \(n\)이 증가함에 따라 표본 평균 \(\bar{X}_n\)이 모평균 \(\mu\)에 수렴하는 현상을 설명하려는 점에서는 공통점이 있습니다. 그래도 각각의 차이를 조금은 이해해 보아야 하겠죠?
큰수의 약법칙(Weak law of large numbers)
i.i.d. 확률변수 수열 중에서 \(n\)번째까지의 확률 변수의 평균 \(\bar{X}_n\)과 모평균 \(\mu\)의 차이의 절대값이 임의의 양수 \(\epsilon\) 보다 클 확률이 0에 수렴한다는 정리(theorem)입니다. 수식으로 나타내면 아래와 같습니다.
\[n \rightarrow \infty \text{ 일때,}\] \[P(|\bar{X}_n - \mu| \gt \epsilon) \rightarrow 0\\\]정리하자면 큰수의 약법칙은 확률 수렴(convergence in probability)에 대해 말하는 것입니다. 확률 수렴이란 \(n\)이 증가함에 따라 확률변수가 특정 상수에 가까워지는 확률값이 특정값에 수렴하는 것을 뜻합니다. 위 식이 의미하는 바를 그림으로 나타내어 보았습니다. 아래 그림을 통해서 큰수의 약법칙은 \(n\)이 증가할 때, 확률 변수인 표본 평균 \(\bar{X}_n\)이 실제 모수인 \(\mu\)의 근처에 존재할 확률이 1에 근사한다는 의미로 해석할 수 있습니다.
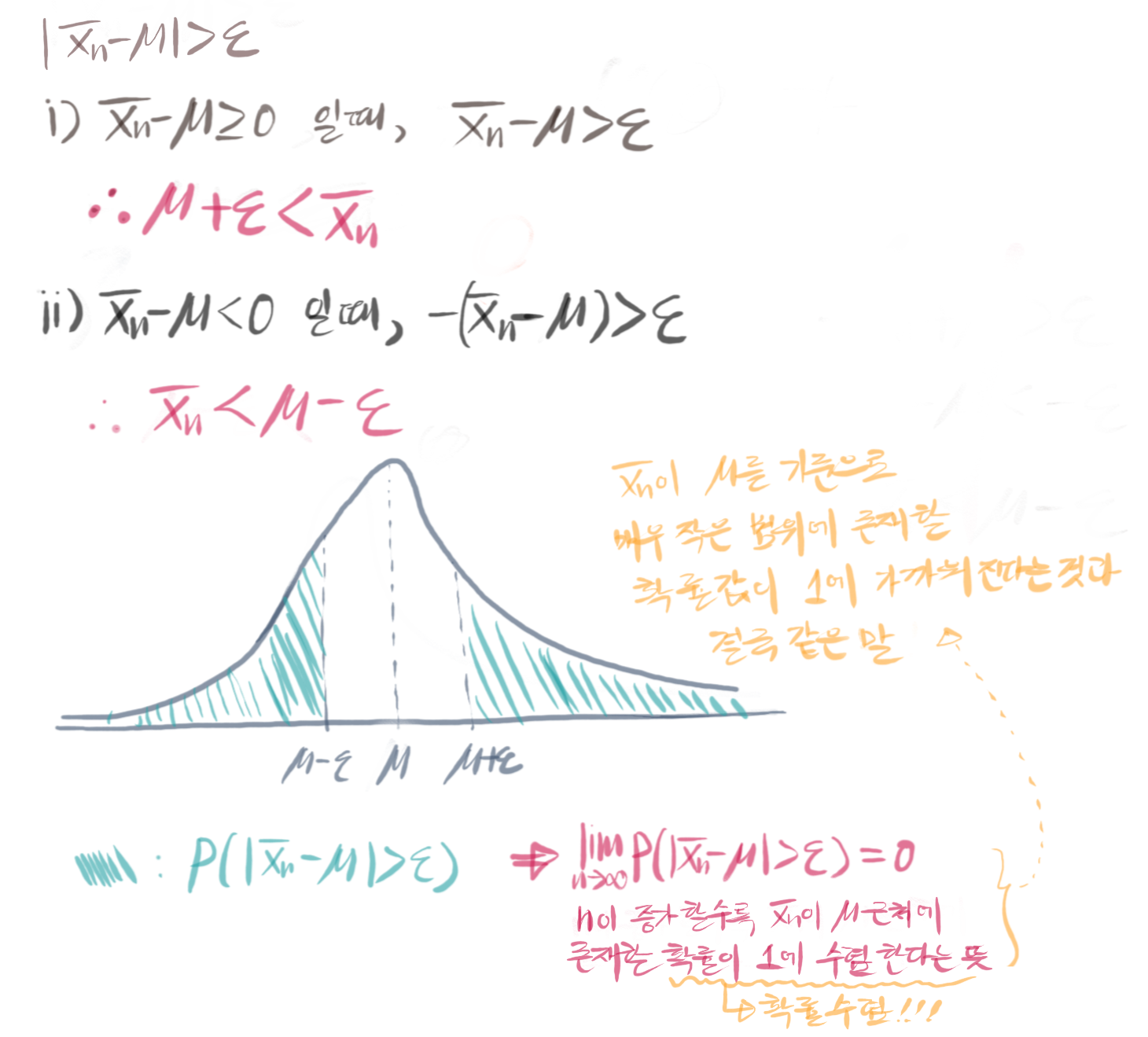
제가 위에서 확률 수렴을 말할 때 특별히 확률이라는 단어를 강조한 이유는 이것이 다음에 설명할 큰수의 강법칙과의 차이점이기 때문입니다. 큰수의 약법칙은 확률값의 수렴을 말하는데 반해 큰수의 강법칙은 확률변수 자체가 수렴한다는 것을 말합니다. 따라서 큰수의 강법칙이 조금 더 강하게 큰수의 법칙을 설명하고 있다고 해석할 수 있습니다.
한편 확률 수렴은 다음의 표기들로도 나타낼 수 있습니다.
\[\bar{X}_n \xrightarrow{p} \mu\] \[\text{plim}_{n \rightarrow \infty} \bar{X}_n = \mu\] \[\lim_{n \rightarrow \infty}\text{Pr}(|\bar{X}_n - \mu| \gt \epsilon) = 0\]큰수의 강법칙(Strong law of large numbers)
큰수읙 강법칙은 다음의 수식으로 요약할 수 있습니다.
\[P(\bar{X}_n \rightarrow \mu) =1\]다시 말해 확률변수인 표본 평균 \(\bar{X}_n\)이 모평균 \(\mu\)에 1의 확률로 수렴한다는 것을 뜻합니다. 큰수의 약법칙에서 언급했던 것처럼 큰수의 강법칙은 확률변수가 수렴한다는 것을 뜻하므로 이 부분에서 큰수의 약법칙과 약간의 차이가 있습니다. 두가지 버전을 구분해서 설명하자면 큰수의 약법칙은 \(n\)이 증가함에 따라 표본 평균 \(\bar{X}_n\)이 존재할 범위가 아주 작은 구간에 점점 집중되어 가는 것을 말하는데 반해 큰수의 강법칙은 표본평균 \(\bar{X}_n\) 자체가 모평균 \(\mu\)에 수렴하는 것을 뜻합니다. 이러한 관점에서 큰수의 강법칙이 조금 더 강하게(?) 큰수의 법칙을 설명하려는 느낌이 있습니다.
2 큰수의 약법칙 증명
큰수의 약법칙은 쳬비셰프 부등식(che… inequality)을 활용하며 쉽게 증명이 가능합니다. 먼저 쳬비셰프 부등식은 다음과 같습니다. 확률 변수 \(X\), 확률 변수의 기대값 \(\mu(=E(X))\), 임의의 양수 \(a(>0)\)가 주어졌을 때,
\[P(|X-\mu|\geq a) \leq \cfrac{\text{Var}(X)}{a^2}\]쳬비셰프 부등식은 마르코프 부등식을 통해 간단하게 유도됩니다. 마르코프 부등식에 대한 내용은 인터넷에 많은 자료 있으니 참고해주세요. 이제 쳬비셰프 부등식을 이용하여 큰수의 약법칙을 간단하게 증명해보겠습니다. 위 식에서 몇몇 변수들을 우리의 목적에 맞게 변환하면 아래의 식이 나타납니다.
\[P(|\bar{X}_n - \mu|>\epsilon) \leq \cfrac{\sigma^2}{n \epsilon^2} \leftarrow \text{Var}(\bar{X}_n) = \cfrac{\sigma^2}{n}\]\(n \rightarrow \infty\)에 따라 우변이 0으로 수렴함을 쉽게 알 수 있으므로 확률 수렴을 뜻하는 큰수의 약법칙이 간단하게 증명되었습니다. 참고로 표본 평균 \(\bar{X}_n\)의 분산이 도출되는 과정이 궁금하시다면 여기를 참고해주세요.
3 예시
동전을 \(n\)번 던지기
i.i.d.인 확률 변수 \(X_1, X_2, \cdots\)가 존재하고 각 확률 변수들의 분포는 \(Bern(1/2)\)를 따른다고 가정해 봅시다. 이때 \(X_j\)를 지시 확률 변수(사건이 발생하면 1, 발생하지 않으면 0을 나타내는 확률 변수)로도 볼 수 있습니다. 왜냐하면 동전기 시행은 앞면이 나오는 사건과 앞면이 아닌 사건(뒷면) 두개만 존재하기 때문에 앞면이 나왔을 때를 1, 뒷면이 나왔을 때를 0으로 볼 수 있습니다. 이러한 상황에서는 표본 평균 \(\bar{X}_n\)을 동전 던지기 시행을 \(n\)번 했을 때, 앞면이 나오는 횟수로 생각 할 수 있습니다. 다시 말해 표본 평균 \(\bar{X}_n\)을 앞면이 나타날 확률로 생각할 수 있다는 것이죠.
큰수의 강법칙(SLLN) 입장에서 보면 확률 변수 \(\bar{X}_n\)이 모평균 \(\mu(=1/2)\)에 수렴할 확률은 \(1\)입니다. 한편 큰수의 약법칙(WLLN)의 입장에서는 시행 횟수 \(n\)이 커질수록 표본평균 \(\bar{X}_n\)과 모평균 \(\mu(=1/2)\)의 차이가 임의의 양수 \(\epsilon\) 보다 클 확률이 점점 작아져 0에 수렴하게 됩니다.
큰수의 법칙을 그래프로 확인해 볼까요? 동전을 300번 던지는 시행을 6번 반복한다고 해봅시다(실제로는 시행 자체는 무한번 하는 것이지만 그래프의 단순화를 위해 임의로 6번으로 하였습니다. 특별한 의미는 없음). 우리가 주목할 점은 6번의 시행의 표본 평균이 동전 던지기 횟수 \(n\)가 증가함에 따라 모평균 \(1/2\)에 실제로 근접해 가는지를 눈으로 확인해 보는 것입니다.
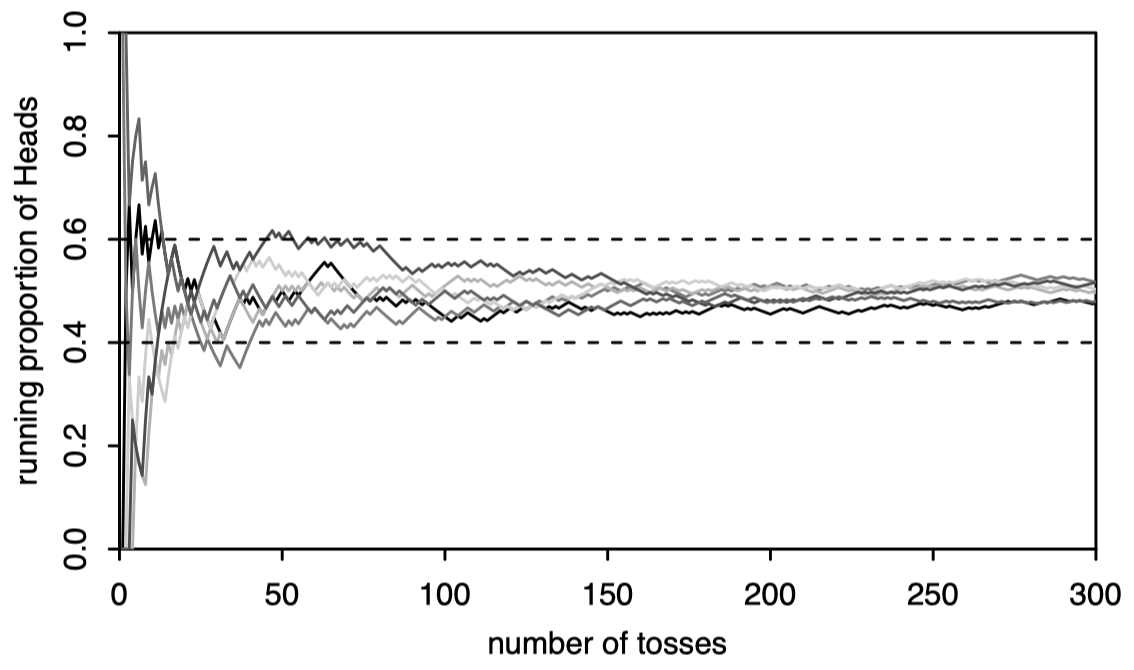\(n\)의 크기가 커질수록(표본의 크기가 커질수록) 표본평균은 모평균에 근사한다는 것이 확실히 보인다!
4 중심 극한 정리와의 차이점
큰수의 법칙과 중심 극한 정리는 공통점도 있고 차이점도 있습니다. 먼저 공통점은 둘다 표본 평균 \(\bar{X}_n\)에 대해 설명한다는 것입니다. 하지만 중요한 차이점이 존재합니다. 지금까지 정리한 큰수의 법칙 내용을 떠올리신다면, 표본 평균 \(\bar{X}_n\)이 \(n \rightarrow \infty\)에 따라 모평균 \(\mu\)에 확률 수렴한다는 이야기는 쭉 진행해 왔지만, 표본 평균 \(\bar{X}_n\)이 따르는 분포에 대해서는 한번도 설명하지 않았다는 사실을 알아 차리실 수 있습니다. 표본 평균 \(\bar{X}_n\)은 확률 변수이므로 당연히 어떤 분포를 따를텐데 말이죠… 분포에 대해 설명하는 이론은 없을까요? 그것이 바로 중심 극한 정리입니다. 중심 극한 정리는 표본 평균 \(\bar{X}_n\)이 \(n \rightarrow \infty\)에 따라 정규 분포로 분포 수렴 한다는 사실을 밝히는 정리입니다. 중심 극한 정리에 대한 내용은 여기를 참고해주세요.
참고자료
- 위키피디아-확률변수의 수렴
- “Introduction to Probability”, Joseph K. Blitzstein, Jessica Hwang