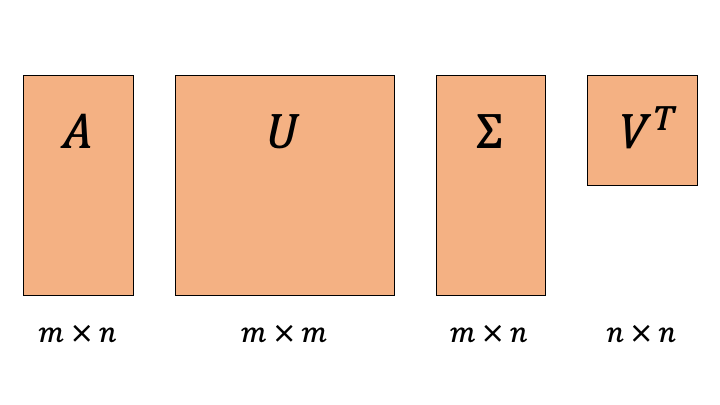행렬을 직교행렬 두개와 대각행렬 하나로 분해할 수 있습니다.

3줄 요약

---

• 특이값 분해(SVD)는 \(m \times n\) 직사각 행렬 \(M\)을 직교행렬 \(U\), \(V^T\)와 고유값 행렬 \(\Sigma\)로 대갹화 하는 방법입니다.
• 고유값 분해(EVD)는 정방 행렬에만 적용 가능한데 반해, 특이값 분해(SVD)는 직사각 행렬에도 적용가능 합니다.
• 데이터 압축, 노이즈 제거, 추천 시스템 등 머신러닝과 관련된 다양한 분야에서 응용되는 중요한 개념입니다.

---

\(m \times n\) 직사각 행렬을 직교 행렬 두개와 고유값 행렬로 대각화 할 수 있는 특이값 분해에 대해 알아보겠습니다. 특이값 분해는 직사각 행렬도 적용할 수 있다는 점에서 정방 행렬만을 대상으로 하는 고유값 분해에 비해 그 활용 범위가 넓다고 할 수 있습니다. 머신러닝을 공부하시는 분들이라면 한번쯤은 들어보셨을 것이라고 생각합니다. 머신러닝과 관련된 정말 여러 분야에서 활용되는 개념이므로 반드시 이해가 필요하다고 생각합니다. 특이값 분해를 이해하기 위해서는 아래의 선수 지식이 요구됩니다.

• 고유값과 고유벡터
• 대칭 행렬(symmetric matrix)
• 직교 행렬(orthogonal matrix)

본 글에서 행렬과 벡터의 표기는 다음을 따릅니다.

• 행렬: \(\boldsymbol{X}\)
• 벡터: \(\boldsymbol{x}\)
• 벡터의 원소: \(x\)

1   SVD(특이값 분해)란?

---

특이값 분해(singular value decomposition)란 \(m \times n\) 직사각 행렬을 아래와 같이 직교 행렬 두 개와 대각 행렬 하나로 대각화 분해하는 기법입니다.

\[\boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T} \tag{1}\]

• \(\boldsymbol{U}\) : \(m \times m\) 정방 행렬

• \(\boldsymbol{\Sigma}\): \(m \times n\) 직사각 대각 행렬

• \(\boldsymbol{V}\): \(n \times n\) 정방 행렬

2   \(\boldsymbol{U}\) 행렬

---

\(\boldsymbol{U}\)는 \(\boldsymbol{A}\boldsymbol{A}^T\)를 고유값 분해(EVD)¹하여 얻을 수 있는 고유 벡터(eigen vector)²들을 열벡터로 가지는 직교 행렬(orthogonal matrix)³입니다. \(\boldsymbol{U}\)의 열벡터들은 직사각 행렬 \(\boldsymbol{A}\)의 left singular vector라고 불립니다. 그렇다면 \(\boldsymbol{U}\)가 어떻게 유도되는지 궁금하지 않으신가요? 대칭 행렬의 고유값 분해의 성질을 활용하면 됩니다.

대칭 행렬의 고유값 분해의 성질을 안다는 가정하에, \(\boldsymbol{A}\boldsymbol{A}^T\)를 통해서 \(\boldsymbol{U}\)를 유도해 보도록 하겠습니다. \(\boldsymbol{A}\boldsymbol{A}^T\)는 대칭 행렬이므로 항상 고유값 분해가 가능합니다 (심지어 직교 행렬로 분해가 가능). 따라서 \(\boldsymbol{A}\boldsymbol{A}^T\)를 고유값 분해하면, 아래와 같은 형태를 가질 것이라고 생각 할 수 있습니다.

\[\boldsymbol{A}\boldsymbol{A}^T=\boldsymbol{MDM}^T \tag{2}\]

• \(\boldsymbol{M}\), \(\boldsymbol{M}^T\): \(\boldsymbol{A}\boldsymbol{A}^T\)의 고유벡터들을 열벡터로 가지는 직교 행렬
• \(\boldsymbol{D}\): \(\boldsymbol{A}\boldsymbol{A}^T\)의 고유값들을 대각 원소로 가지는 대각 행렬

그리고 위에서 언급한 \((1)\) 식을 활용해서 \(\boldsymbol{A}\boldsymbol{A}^T\)를 구해 보면 다음과 같이 수식을 전개할 수 있습니다.

\[\begin{align} \boldsymbol{A}\boldsymbol{A}^T &=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T}(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T})^T \\[1em] &=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T} \boldsymbol{V} \boldsymbol{\Sigma}^T \boldsymbol{U}^T \\[1em] &=\boldsymbol{U} (\boldsymbol{\Sigma}\boldsymbol{\Sigma}^T) \boldsymbol{U}^T \tag{3} \end{align}\]

그렇다면, \((2)\) 식과 \((3)\) 식이 매우 비슷한 꼴이라는 것을 발견하셨나요? 이를 통해 처음에 유도하려고 했던 \(\boldsymbol{U}\)는 \(\boldsymbol{A}\boldsymbol{A}^T\)의 고유벡터들을 열벡터로 가지는 행렬이라는 것을 알 수 있네요!

3   \(\boldsymbol{V}\) 행렬

---

\(\boldsymbol{V}^T\)는 \(\boldsymbol{A}^T\boldsymbol{A}\)를 고유값 분해(EVD)하여 얻을 수 있는 고유 벡터(eigen vector)들을 행벡터로 가지는 직교 행렬(orthogonal matrix)입니다. \(\boldsymbol{V}^T\)의 행벡터들은 직사각 행렬 \(\boldsymbol{A}\)의 right singular vector라고 불립니다.

\(\boldsymbol{V}^T\)를 유도하는 것은 \(\boldsymbol{U}\)를 유도하는 과정과 사실상 거의 동일합니다. \(\boldsymbol{A}^T\boldsymbol{A}\)에 대해 고유값 분해를 한다는 점만 다릅니다(\(\boldsymbol{U}\)는 \(\boldsymbol{A}\boldsymbol{A}^T\)에 대한 고유값 분해였죠). 결과만 보면, \(\boldsymbol{A}^T\boldsymbol{A}\)를 고유값 분해하면 다음과 같은 식을 얻을 수 있습니다.

\[\boldsymbol{A}^T\boldsymbol{A} = \boldsymbol{V}(\boldsymbol{\Sigma}^T\boldsymbol{\Sigma})\boldsymbol{V}^T \tag{4}\]

다시 말해 \(\boldsymbol{V}^T\)는 \(\boldsymbol{A}^T\boldsymbol{A}\)의 고유벡터들을 행벡터로 가지는 행렬이라는 것을 알 수 있습니다.

4   \(\boldsymbol{\Sigma}\) 행렬

---

\(m \gt n\) 일 때의 \(\Sigma\) 행렬의 형상. AskPython

\(\boldsymbol{\Sigma}\)는 \(\boldsymbol{A}\boldsymbol{A}^T\) 또는 \(\boldsymbol{A}^T\boldsymbol{A}\) 행렬의 고유값(eigen value)들의 제곱근(square root)으로 이루어진 \(m \times n\) 직사각 대각 행렬입니다. \(\boldsymbol{A}\boldsymbol{A}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)는 공통의 고유값 \(\sigma^2_{1} \ge \sigma^{2}_2 \ge \cdots \ge \sigma^2_{r} \ge 0\) \((\)단, \(r = \text{min}(m, n)\)\()\)을 가집니다 (이유는 잠시 뒤에 나옵니다). 이들의 값에 루트를 씌워 얻은 \(\sigma \ge \sigma_2 \ge \cdots \ge \sigma_r \ge 0\)을 대각 원소로 가지는 \(m \times n\) 행렬이 바로 SVD에 찾으려는 \(\Sigma\) 행렬입니다. 그리고 이 행렬의 원소들을 singular value라고 합니다.

왜 제곱근을 씌울까요? 먼저 대각 행렬 거듭제곱의 성질을 알아야 하겠습니다. 대각 행렬 자체를 \(n\) 제곱하는 것은 단순히 대각 성분들을 \(n\) 제곱한 것과 같은 결과입니다.

\[D = \left[\begin{matrix} \sigma_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{mn} \end{matrix} \right] \text{일 때,}\]

\[D^{n} = \left[\begin{matrix} \sigma_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{mn} \end{matrix} \right]^{n} = \left[\begin{matrix} \sigma_{11}^{n} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{mn}^{n} \end{matrix} \right]\]

다시 제곱근을 씌우는 이유를 설명해볼게요. \(\boldsymbol{A}\boldsymbol{A}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\) 의 고유값으로 이루어진 행렬은 식 \((3)\)과 \((4)\)에서 보았듯이, 각각 \(\boldsymbol{\Sigma}\boldsymbol{\Sigma}^T\)와 \(\boldsymbol{\Sigma}^T\boldsymbol{\Sigma}\)입니다. 또한 특이값 분해의 정의에서 언급 했듯이, \(\boldsymbol{\Sigma}\)는 직사각 대각 행렬이므로 대각 행렬의 거듭 제곱 성질을 당연히 따르게 됩니다.

최종적으로 \(\boldsymbol{\Sigma}\boldsymbol{\Sigma}^T\)와 \(\boldsymbol{\Sigma}^T\boldsymbol{\Sigma}\)는 \(\boldsymbol{\Sigma}^2\)과 같은 표현이라는 점을 알고 계시다면 (간단한 예시를 들어 계산 해보시면 쉽게 이해할 수 있어요), 우리가 알고 싶은 \(\boldsymbol{\Sigma}\) 행렬은 \(\boldsymbol{\Sigma}\boldsymbol{\Sigma}^T\) 또는 \(\boldsymbol{\Sigma}^T\boldsymbol{\Sigma}\)의 원소들의 제곱근(square root)임을 도출할 수 있겠습니다.

4.1   \(\boldsymbol{A}\boldsymbol{A}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)의 고유값은 동일합니다.

\(\boldsymbol{A}\boldsymbol{A}^T\)의 고유값을 \(\lambda\)라고 하고 고유벡터를 \(\boldsymbol{v}(\neq \boldsymbol{0})\)라고 하면, 고유값과 고유벡터의 정의에 따라 아래 수식이 성립합니다.

\[(\boldsymbol{A}\boldsymbol{A}^T)\boldsymbol{v} = \lambda \boldsymbol{v}\]

양변에 \(\boldsymbol{A}^T\)를 곱하면 아래의 수식을 유도할 수 있습니다.

\[(\boldsymbol{A}^T\boldsymbol{A})(\boldsymbol{A}^T\boldsymbol{v}) = \lambda(\boldsymbol{A}^T \boldsymbol{v})\]

위 수식을 볼때, \(\boldsymbol{A}\boldsymbol{A}^T\)과 \(\boldsymbol{A}^T\boldsymbol{A}\)의 고유값은 동일하다는 사실을 이끌어 낼 수 있습니다.

4.2   \(\boldsymbol{A}\boldsymbol{A}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)의 고유값은 항상 0 이상의 값을 가집니다.

이는 두가지 방식으로 증명할 수 있습니다. 그리 어렵지 않으니 꼭 천천히 읽어 봐주세요.

방법1. \(\boldsymbol{A}\boldsymbol{A}^T\)의 고유값을 \(\lambda\)라고 하고 고유벡터를 \(\boldsymbol{v}(\neq \boldsymbol{0})\)라고 하면, 고유값과 고유벡터의 정의에 따라 아래 수식이 성립합니다.

\[\boldsymbol{A}\boldsymbol{A}^T\boldsymbol{v} = \lambda \boldsymbol{v}\]

양변에 \(\boldsymbol{v}^T\)를 곱하면 아래의 수식을 유도할 수 있습니다.

\[\begin{align} \boldsymbol{v}^T\boldsymbol{A}\boldsymbol{A}^T\boldsymbol{v} &= \lambda \boldsymbol{v}^T \boldsymbol{v} \\[1em] (\boldsymbol{A}^T\boldsymbol{v})^T\boldsymbol{A}^T\boldsymbol{v} &= \lambda \boldsymbol{v}^T \boldsymbol{v} \\[1em] \Vert \boldsymbol{A}^T\boldsymbol{v} \Vert^{2} &= \lambda \Vert \boldsymbol{v} \Vert^{2} \end{align}\]

\(\Vert \boldsymbol{A}^T\boldsymbol{v} \Vert^{2} \ge 0\) 이고, \(\Vert \boldsymbol{v} \Vert^{2} \gt 0\) \((\because \boldsymbol{v}\neq \boldsymbol{0})\)이므로 항상 \(\lambda \ge 0\) 임을 알 수 있습니다. 같은 과정을 \(\boldsymbol{A}^T\boldsymbol{A}\) 행렬에 적용해도 결국 고유값은 항상 0 이상이라는 동일한 결과를 얻을 수 있습니다.

방법 2. positive semi-definite matrix 행렬은 항상 0이상의 고유값을 가진다는 성질을 활용하여 증명 가능합니다. positive semi definite matrix는 대칭 행렬(symmetric matrix)에서만 정의 되는 개념인데요. 다음의 수식을 만족하는 대칭 행렬 \(\boldsymbol{A}\)를 positive semi-definite matrix라고 하며, positive semi-definite matrix는 항상 0 이상의 고유값을 가지는 성질이 있습니다.

\[\forall \boldsymbol{x} \neq0, \space \boldsymbol{x}^T\boldsymbol{A}\boldsymbol{x} \ge0\]

먼저 \(\boldsymbol{AA}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)가 대칭 행렬인지 알아보죠.

\[(\boldsymbol{AA}^T)^T = \boldsymbol{A}\boldsymbol{A}^T\] \[(\boldsymbol{A}^T\boldsymbol{A})^T = \boldsymbol{A}^T\boldsymbol{A}\]

대칭 행렬의 정의에 따라, 두 행렬은 대칭 행렬임을 알 수 있습니다. 그렇다면 positive semi-definite matrix 인지만 확인하면 고유값이 항상 0 이상이라는 사실을 알 수 있겠습니다.

\[\boldsymbol{x}^T\boldsymbol{AA}^T\boldsymbol{x} = (\boldsymbol{A}^T\boldsymbol{x})^T(\boldsymbol{A}^T\boldsymbol{x}) \ge 0\] \[\boldsymbol{x}^T\boldsymbol{A}^T\boldsymbol{A}\boldsymbol{x} = (\boldsymbol{Ax})^T(\boldsymbol{Ax}) \ge 0\]

따라서 \(\boldsymbol{AA}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)는 positive semi-definite 행렬임을 쉽게 알 수 있습니다. 이는 곧 \(\boldsymbol{AA}^T\)와 \(\boldsymbol{A}^T\boldsymbol{A}\)가 항상 0 이상의 고유값을 가진다는 사실을 증명한 것입니다.

5   Reduced SVD

---

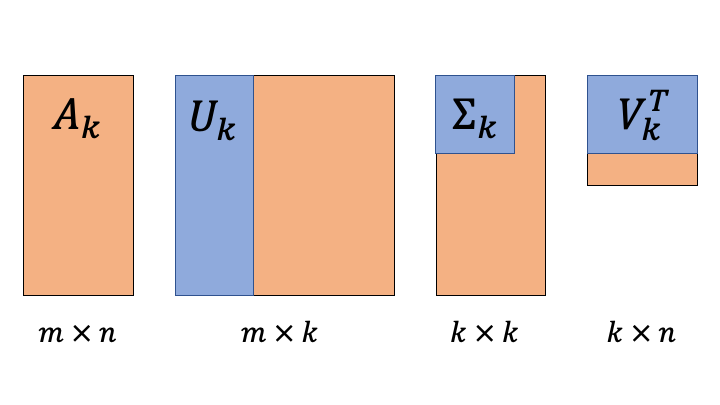일부의 고유값만 취하여 원 행렬을 근사하는 행렬을 계산할 수 있습니다.

사실 SVD는 행렬을 분해하는 과정 보다는 부분 정보만 활용하여 복원하는 과정에서 그 활용성이 빛나는 것 같습니다. 이와 같은 방법을 통해 데이터 압축, 노이즈 제거 등의 기법을 구현할 수 있게 됩니다. 특히 추천 시스템은 원 행렬의 크기가 커질수록 연산량이 기하급수적으로 증가하게 되는데, 일부의 정보 (일부의 고유값)만을 활용한다면 연산량을 획기적으로 낮춰서 원 행렬을 근사할 수 있게 됩니다. 물론 일부의 정보를 활용한다는 사실 때문에 원 행렬과 근사 행렬 간의 오차가 발생할 수는 있습니다.

행렬을 복원은 일부의 값만 활용하여 다음과 같이 layer를 쌓는 것과 동일하게 생각해볼 수 있습니다. 먼저 행렬 \(\boldsymbol{A}(m \gt n)\)가 SVD를 거쳐 아래와 같이 분해 되었다고 생각해보죠. 지금까지는 위에서 언급한 일반적인 SVD와 관련된 내용입니다.

\[\boldsymbol{A} = \boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T = \left[\begin{matrix} \vert & & \vert \\ \boldsymbol{u}_1 & \cdots & \boldsymbol{u}_{m} \\ \vert & & \vert \end{matrix} \right] \left[\begin{matrix} \sigma_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{n} \\ 0 & \cdots & 0 \end{matrix} \right] \left[\begin{matrix} - & \boldsymbol{v}_{1}^{T} &- \\ & \vdots & \\ - & \boldsymbol{v}_{n}^{T} &- \end{matrix} \right]\]

그렇다면 어떻게 해야 원 행렬 \(\boldsymbol{A}\)와 같은 크기를 유지하면서도 ‘일부’의 정보만을 활용해서 연산량을 줄이는 방향으로 행렬 근사를 할 수 있을까요? \(\boldsymbol{U}\) 행렬과 \(\boldsymbol{V}^T\) 행렬을 건들면 원 행렬 \(\boldsymbol{A}\)와 크기가 달라져 버릴 것만 같습니다. 해결책은 \(\boldsymbol{\Sigma}\) 행렬의 크기를 조작하는 것입니다. 현재 \(\boldsymbol{\Sigma}\) 행렬에는 크기의 내림 차순으로 \(n\)개의 고유값이 대각 성분에 정렬되어 있는 상태입니다. 여기서 \(k(<n)\)개의 고유값만 취해보는 것이죠. 이는 정보량이 큰 상위 \(k\)개의 값만 활용하는 것으로 해석 할 수 있습니다.

본론으로 돌아와서 \(k\)개의 고유값만 활용하게 된다면 행렬 연산이 어떻게 변하는지 살펴봅시다.

\[\boldsymbol{A}_k = \boldsymbol{U}_k\boldsymbol{\Sigma}_k\boldsymbol{V}^T_k = \left[\begin{matrix} \vert & & \vert \\ \boldsymbol{u}_1 & \cdots & \boldsymbol{u}_{k} \\ \vert & & \vert \end{matrix} \right] \left[\begin{matrix} \sigma_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{k} \end{matrix} \right] \left[\begin{matrix} - & \boldsymbol{v}_{1}^{T} &- \\ & \vdots & \\ - & \boldsymbol{v}_{k}^{T} &- \end{matrix} \right]\] \[\boldsymbol{A}_k \in \mathbb{R}^{m \times n}\] \[\boldsymbol{U}_k \in \mathbb{R}^{m \times k}\] \[\boldsymbol{\Sigma}_k \in \mathbb{R}^{k \times k}\] \[\boldsymbol{U}_k \in \mathbb{R}^{k \times n}\]

이렇게 큰 정보량을 가지는 고유값 \(k\)개를 선택하여 근사 복원한 행렬 \(\boldsymbol{A}_k\)는 원 행렬 \(\boldsymbol{A}\)와 같은 크기를 유지하면서도, 연산량을 줄일 수 있는 이점이 있습니다. 물론 그 만큼의 정보의 손실을 발생한다는 단점이 있겠네요.

마지막으로 SVD를 통해 분해된 행렬과 reduced SVD의 행렬 notation은 다음과 같이 덧셈 notation으로도 나타낼 수 있습니다.

\[\boldsymbol{A} = \sigma_{1}\boldsymbol{u}_{1}\boldsymbol{v}^T_1 + \cdots + \sigma_{n}\boldsymbol{u}_{n}\boldsymbol{v}^T_{n}\] \[\boldsymbol{A}_k = \sigma_{1}\boldsymbol{u}_{1}\boldsymbol{v}^T_1 + \cdots + \sigma_{k}\boldsymbol{u}_{k}\boldsymbol{v}^T_{k}\]

Reference

---

• Singular-value decomposition, Orelly
• 특잇값 분해, 위키피디아 한국어판
• Singular value decomposition, wikipedia
• 특이값 분해(SVD), 공돌이의 수학정리노트
• 특이값 분해(Singular Value Decomposition, SVD)의 활용, 다크 프로그래머
• 특이값 분해 (SVD, Singular Value Decomposition), R Friend
• 선형대수학 - 특이값 분해 SVD(Singular Value Decomposition), 하루하루
• SVD (특이값 분해), 하고 싶은 일을 하자
• 특이값 분해(SVD)의 증명, Deep Campus
• Notes on singular value decomposition for Math 54
• Non-zero eigenvalues of \(\boldsymbol{AA}^T\) and \(\boldsymbol{A}^T \boldsymbol{A}\)
• SVD 를 활용한 협업필터링
• Vozalis, M. G., & Margaritis, K. G. (2005, September). Applying SVD on item-based filtering. In 5th International Conference on Intelligent Systems Design and Applications (ISDA’05) (pp. 464-469). IEEE

footnote

---